Example 1 Graph the logarithmic function f(x) = log 2 x and state range and domain of the function Solution Obviously, a logarithmic function must have the domain and range of (0, infinity) and (−infinity, infinity) Since the function f(x) = log 2 x is greater than 1, we will increase our curve from left to right, a shown below Horizontal Movement If you want to find out if the graph will move either left or right, consider y=f (x±c) If c is negative, the graph moves to the right If c is positive, the graph moves to the left As an example, if I have f (x)= (x3) 3,A General Note Graphical Interpretation of a Linear Function In the equation latexf\left(x\right)=mxb/latex b is the yintercept of the graph and indicates the point (0, b) at which the graph crosses the yaxis;
Linear Functions And Their Graphs
Y=f(x) graph examples
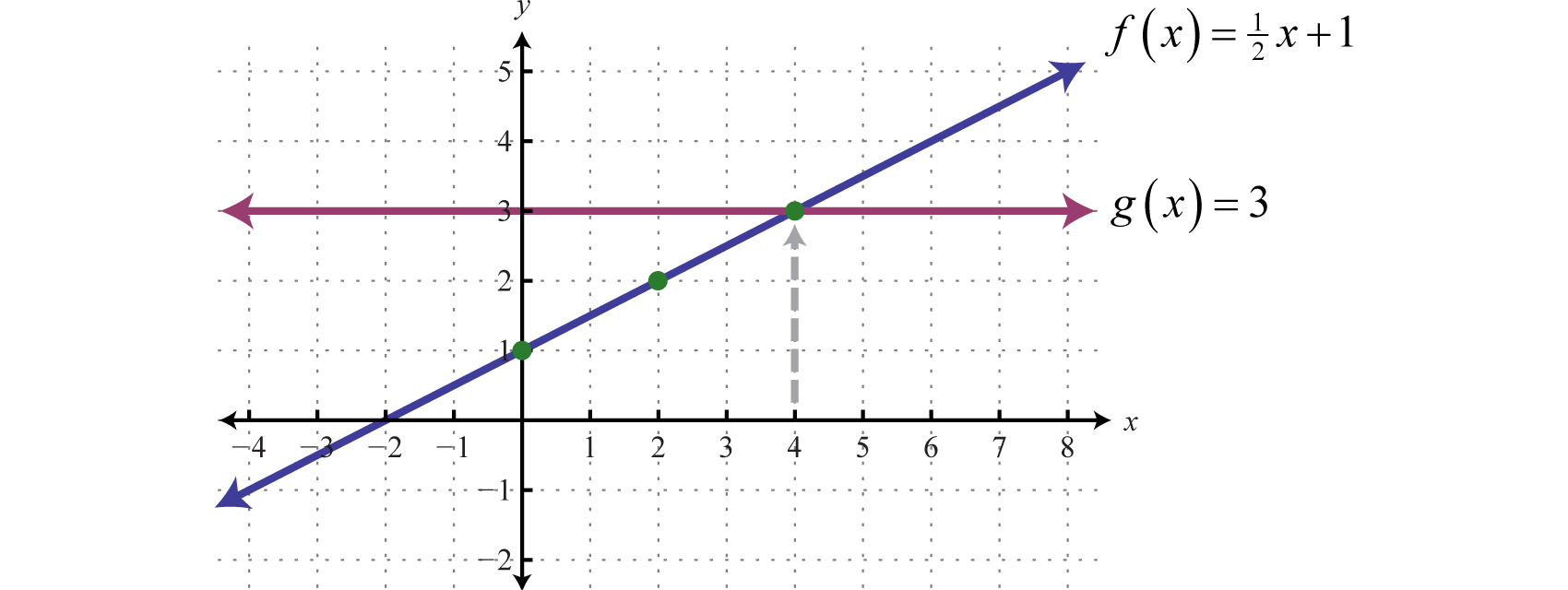
Y=f(x) graph examples-Example 6 Graph f (x) = 1 2 x 1 and g (x) = 3 on the same set of axes and determine where f (x) = g (x) Solution Here f is a linear function with slope 1 2 and yintercept (0,1) The function g is a constant function and represents a horizontal line Graph both ofLet us start with a function, in this case it is f(x) = x 2, but it could be anything



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
F ( x) = x2 A function transformation takes whatever is the basic function f (x) and then "transforms" it (or "translates" it), which is a fancy way of saying that you change the formula a bit and thereby move the graph around For instance, the graph for y = x2 3 looks like this This is three units higher than the basic quadratic, f (x) = x2To graph a function in the xy plane, we represent each input x and its corresponding output f ( x) as a point ( x, y ), where y = f ( x ) In other words, you use the x axis for the input and the y axis for the output The following video shows how to sketch the graph of six basic functions f ( x) = x, f ( x) = x2, f ( x) = x3, f ( xM is the slope of the line and indicates the vertical displacement (rise) and horizontal displacement (run) between each successive pair of points
Y is the output measure, such as process cycle time or customer satisfaction f is the letter representing "function" (what the value (s) of X (s) does/do for Y (the output) X (s) is/are any process input (s) (variables) having assigned or inherent values (s) that is/are involved in producing the output For example, if you call your major department store to ask a question, the ability to have your question answered (Y) is a function (fThe graph of y = f (x) is the graph of y = f (x) reflected about the yaxis Here is a picture of the graph of g(x) =(05x)31 It is obtained from the graph of f(x) = 05x31 by reflecting it in the yaxis Summary of Transformations To graph Draw the graph of f and Changes in the equation of y = f(x) Vertical Shifts y = f (x) cThe graph of f(x) in this example is the graph of y = x2 3 It is easy to generate points on thegraph Choose a value for the first coordinate, then evaluate f at that number to find the second coordinate Thefollowing table shows several values for x
Differentiation is the action of computing a derivative The derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change of the variable xIt is called the derivative of f with respect to xIf x and y are real numbers, and if the graph of f is plotted against x, derivative is the slope of this graph at eachF (x) = x3 Let y = x3 Let us find the inverse function, for that we have to solve for x x = y1/3 Now we have to replace "x" by "f1(x)" and "y" by "x" f1(x) = x1/3 By finding inverse of the given function, we get the other function Note The graph of y = f−1(x) is the reflection of the graph of f in y = xThe output f (x) is sometimes given an additional name y by y = f (x) The example that comes to mind is the square root function on your calculator The name of the function is \sqrt {\;\;} and we usually write the function as f (x) = \sqrt {x} On my calculator I input x for example by pressing 2 then 5 Then I invoke the function by pressing




Graphing Functions With Excel




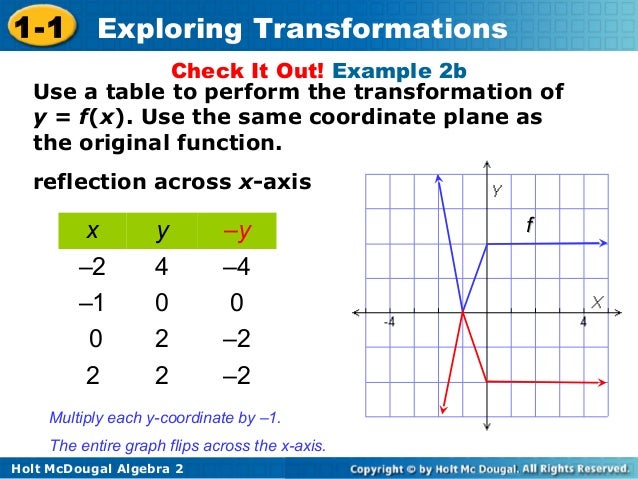
Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
Translations of Functions Suppose that y = f(x) is a function and c > 0;Again, this graph has the line y = 0 as an asymptote Variations on the General Graph Note that if b is negative, the curve will curve downward as the x values increase Note that if the exponent is negative, the curve will tend upward in the negative x values Consider these basic forms for y = −2 x and y = 2 −x respectivelyA function →, with domain X and codomain Y, is bijective, if for every y in Y, there is one and only one element x in X such that y = f(x) In this case, the inverse function of f is the function f − 1 Y → X {\displaystyle f^{1}\colon Y\to X} that maps y ∈ Y {\displaystyle y\in Y} to the element x ∈ X {\displaystyle x\in X} such that y = f ( x )




Graphing Functions Free Sat Training
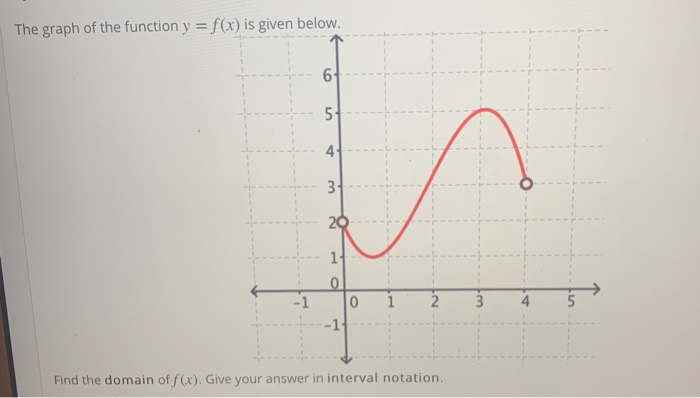



The Graph Of The Function Y F X Is Given Below B Chegg Com
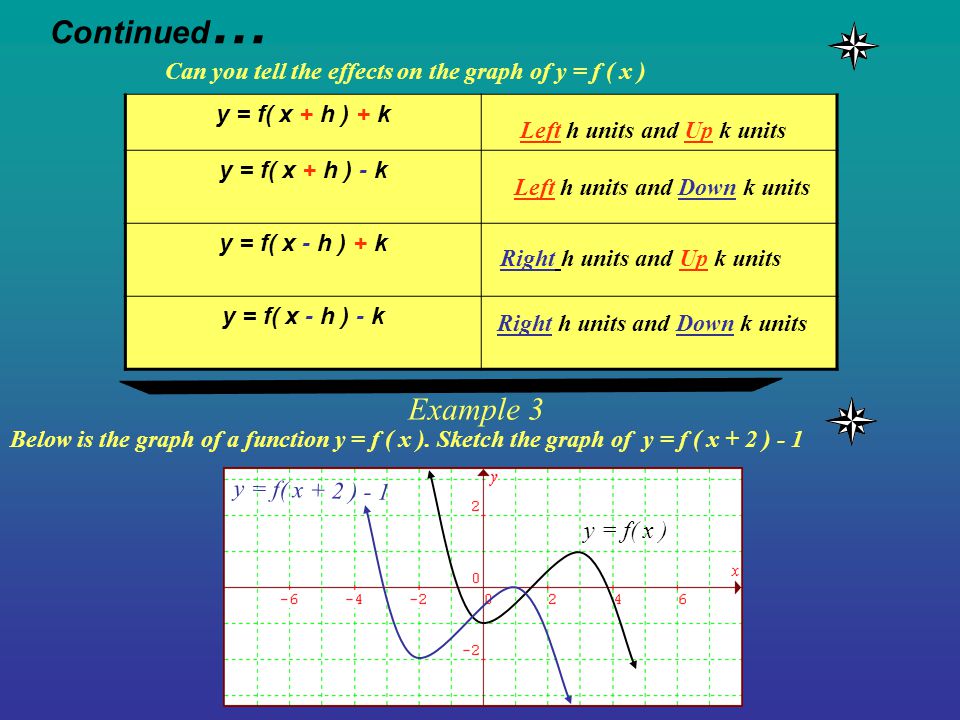
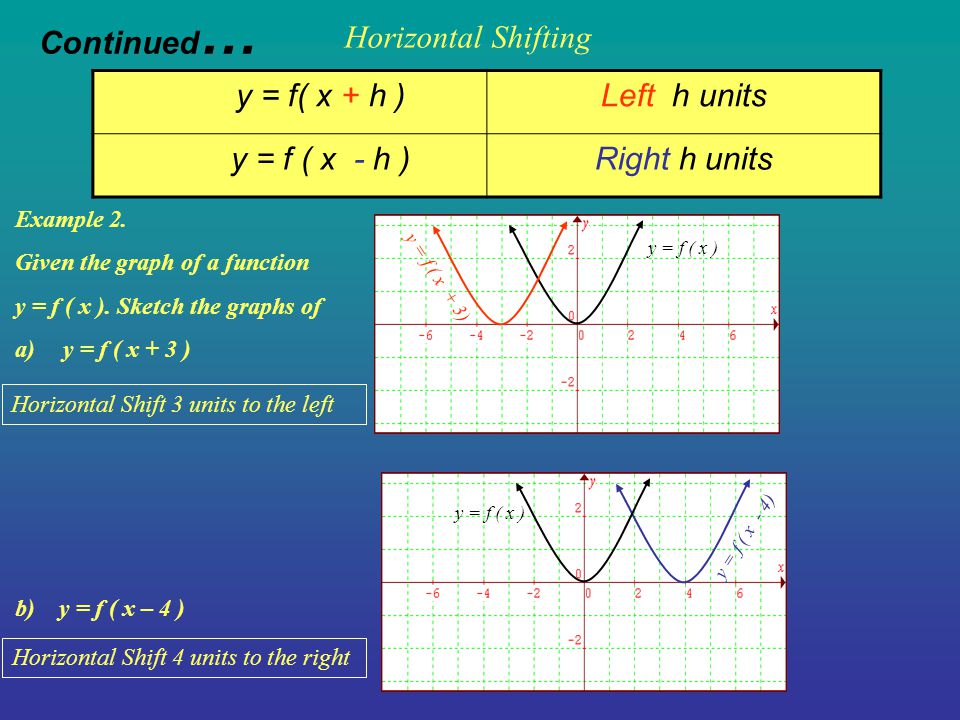
Example 1 From the graph of f ( x ), draw a graph of its derivative f ' ( x ) Since f is a line, its slope is constant Moreover Since f is sloping upward, its slope is a positive constant This means f ' ( x) is a positive constant function Show Next StepConverting from rectangular to parametric can be very simple given y = f (x), the parametric equations x = t, y = f (t) produce the same graph As an example, given y = x 2x6, the parametric equations x = t, y = t 2t6 produce the same parabola However, other parameterizations can be usedSection 56 Graphical Transformations In this section we are going to explore the graphical repercussions of alterations to a given function formula Specifically, we are going to explore how the graph of the function \(g\) compares to the graph \(f\) where



Discontinuous Functions



College Algebra Chapter 2 Functions And Graphs Ppt Download
1 You are correct, given any function f ( x), you get the graph of f ( x ) by taking the graph of f, deleting the graph where x < 0, then reflecting the graph where x > 0 into the region you deleted To understand the answer described in your second paragraph, think of f ( x − 1 ) as g ( x − 1) where we define g as the new function gThe graph of a function w = f(x,y,z) of three variables lies in 4dimensional space, and so we will not attempt to render its graph The level surfaces of w = f(x,y,z) are the surfaces determined by the equation f(x,y,z) = k for values of k in the range of f Example The range of the function w = f(x,y,z) = x2 3y2 5z2 is the set ofExamples • The graph of f(x)=x2 is a graph that we know how to draw It's drawn on page 59 We can use this graph that we know and the chart above to draw f(x)2, f(x) 2, 2f(x), 1 2f(x), and f(x) Or to write the previous five functions



Graphing Calculator Graphing Examples




Graphing Psat Math
I am a graduate student teaching college algebra at a larger state school, and currently I'm covering transformations of graphs of function, ieIn this section we graph seven basic functions that will be used throughout this course Each function is graphed by plotting points Remember that f(x) = y and thus f(x) and y can be used interchangeably Any function of the form f(x) = c, where c isGraph y = x Solution Draw y = x on x ≥ 0 ↓ Draw the image of the line under the reflection in the yaxis ↓ Close Example y = f(x) Graph y = 2x 3 Solution y = 2 x 3 There's x Then first draw y = 2x 3 on x ≥ 0 Linear Equation (Two Variables)



Injective Function Wikipedia



Use The Graph Of A Function To Graph Its Inverse College Algebra
Also, if there is more than one exponential term in the function, the graph may look differentThe following are a couple of examples, just to show you how they work Graph y = 3×2 –x2 Because the power is a negative quadratic, the power is always negative (or zero)Example 1 Let f ( x, y) = x 2 − y 2 We will study the level curves c = x 2 − y 2 First, look at the case c = 0 The level curve equation x 2 − y 2 = 0 factors to ( x − y) ( x y) = 0 This equation is satisfied if either y = x or y = − x Both these are equations for lines, so the level curve for c = 0 is two lines If youThe graph of y = f(x) c is obtained by translating the graph of y = f(x) c units upwards;



Shifting Of Graphs Transformation Example 1 Y F X Kup K Units Y F X Kdown K Units Vertical Shifting Below Is The Graph Of A Function Y Ppt Download
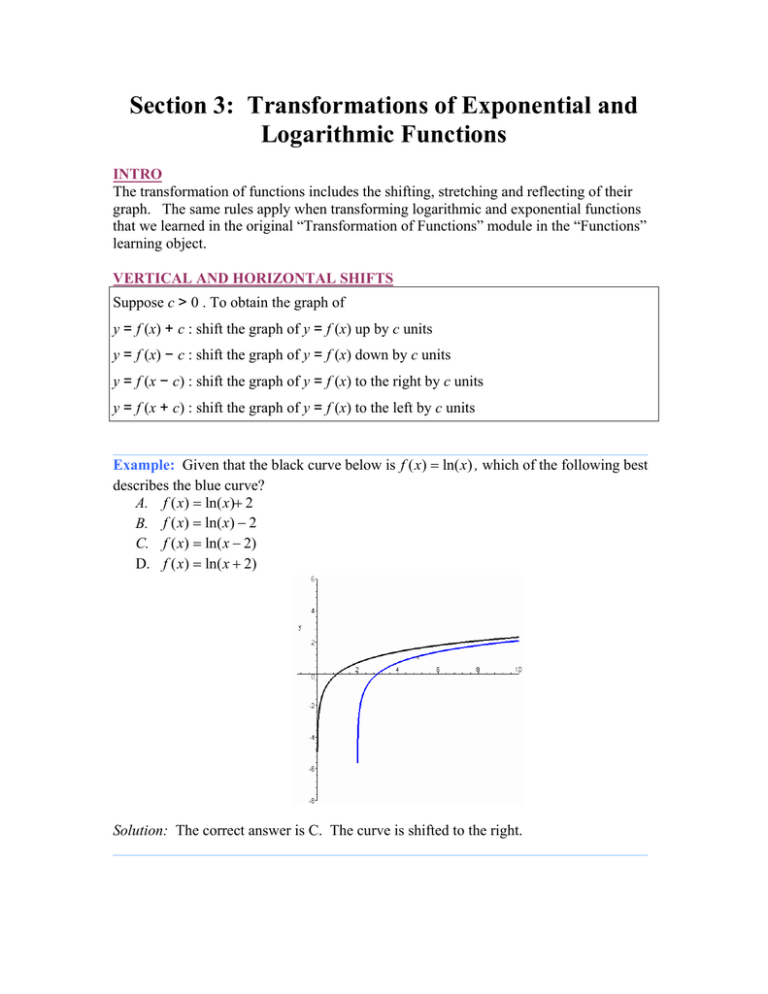



Section 3 Transformations Of Exponential And Logarithmic Functions
Y = kx n In your country let us know!Beneath each designated xvalue, write the corresponding yvalue which is found by using the original equation y = f(x) These ordered pairs (x, y) will be a starting point for the graph of f This completes the sign chart for f' Establish a sign chart (number line) for f'' in the exact same mannerThe graph of y = f(x c) is obtained by translating the graph of y = f(x) c units to the left;



If The Minimum Point On The Graph Of The Equation Y F X Is 1 3 What Is The Minimum Point On He Graph Of The Equation Y F X 5 How Would I Go Enotes Com



2
Free graphing calculator instantly graphs your math problems(ii) The graph y = f(−x) is the reflection of the graph of f about the yaxis (iii) The graph of y = f −1 (x) is the reflection of the graph of f in y = x Translation A translation of a graph is a vertical or horizontal shift of the graph that produces congruent graphs The graph of y = f(x c), c > 0 causes the shift to the left y We may express y directly in terms of x (the argument) by an analytical expression in x We then call y an explicit function of x Example y=x^{2}, y=x\sqrt{x}, y=x7 etc Implicit function When a function (y) is not directly written as a function x but written as a function of x and y then it is called an Implicit function Example y^{2



Linear Function Definition Graphs Properties Solved Examples




Vertical Shifts Let C Represent A Positive Number How The Function Is
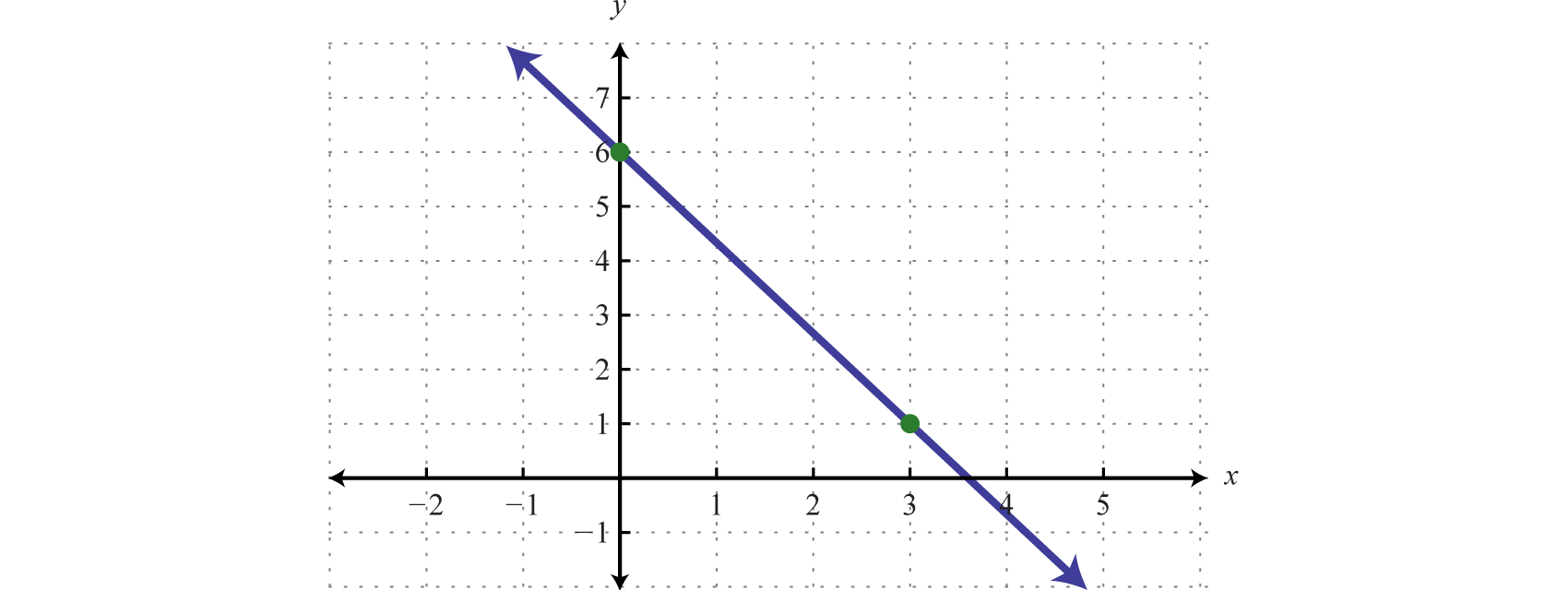
But it all means the same thing, just different letters Slope (Gradient) of a Straight Line Y Intercept of a Straight Line Test Yourself Explore the Straight Line Graph Straight Line Graph Calculator Graph IndexThen the graph of y = f(x c) is obtained by translating the graph of y = f(x) c units to the right;Linear functions have the form f(x) = ax b, where a and b are constants In Figure 111, we see examples of linear functions when a is positive, negative, and zero Note that if a > 0, the graph of the line rises as x increases In other words, f(x) = ax b is increasing on ( − ∞, ∞)



Integration Area And Curves



Mathematics Calculus
On the graph of a line, the slope is a constant The tangent line is just the line itself So f' would just be a horizontal line For instance, if f (x) = 5x 1, then the slope is just 5 everywhere, so f' (x) = 5 Then f'' (x) is the slope of a horizontal linewhich is 0 So f'' (x) = 0 See if you can guess what the third derivative is, or Example 5 Determine if f(x) = 2x 3 – 1 is a one to one function using the algebraic approach Solution Recall that for a function to be a one to one function, f(x 1) = f(x 2) if and only if x 1 = x 2 For us to check if f(x) is a one to one function, let's find the respective expressions for x 1 and x 2 first f(x 1) = 2 x 1 3 – 1 fFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor



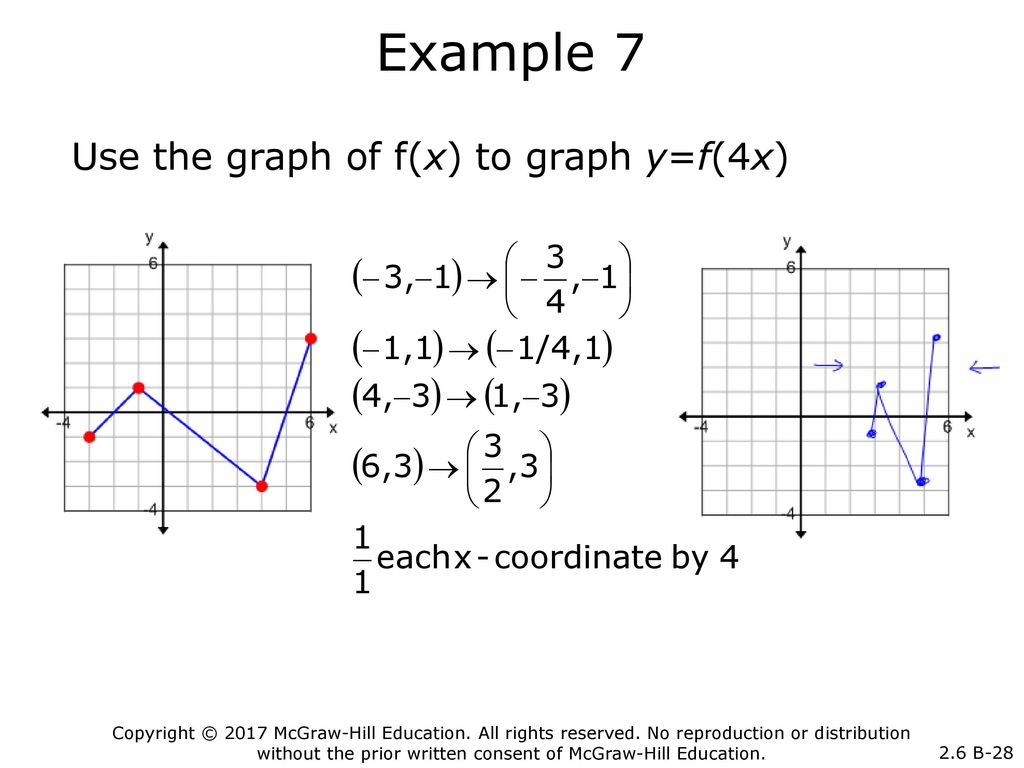
Compress Or Stretch Function Horizontally F Cx Expii
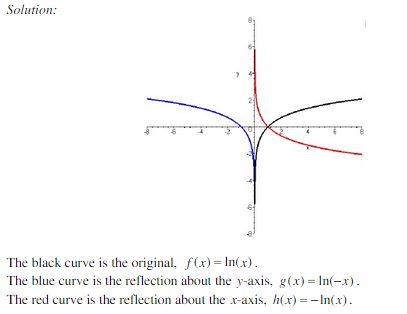



Transformation Of Exponential And Logarithmic Functions Nool
9 rows The most common graphs name the input value x x and the output value y y, and we say yBasic Examples The graph of an exponential function is a strictly increasing or decreasing curve that has a horizontal asymptote Let's find out what the graph of the basic exponential function y = a x y=a^x y = ax looks like (i) When a > 1, a>1, a > 1, the graph strictly increases as xWe say that a function is onetoone if, for every point y in the range of the function, there is only one value of x such that y = f(x) f(x) = x 2 is not one to one because, for example, there are two values of x such that f(x) = 4 (namely –2 and 2) On a graph, a function is one to one if any horizontal line cuts the graph only once



Quadratic Equations With Absolute Value



Http Calculus7 Com Sitebuildercontent Sitebuilderfiles Bsc3dgrphs Pdf
We give the graphs of f ()xx= and gx x( )=− together below for easy reference f ()xx= gx x( )=− The graphs of f ()xx= and gx x( )=− above can be used to graph shifts and scalings of f ()xx= Example The graph of the function gx x() 2 1 3= −− can be given in 3 stepsWe start by graphing the function f 2xx= by scaling the graph of x by a factor of 2



Level Sets Math Insight



Www Scg Ac Uk Pre Enrolment Home Learning Maths Worksheets 1f Translating Graphs




3 Ways To Graph A Function Wikihow




Cc Constructing Accurate Graphs Of Antiderivatives
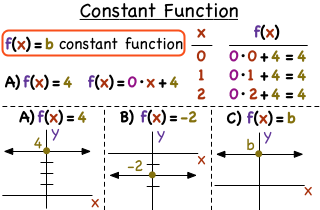



What Is A Constant Function Printable Summary Virtual Nerd




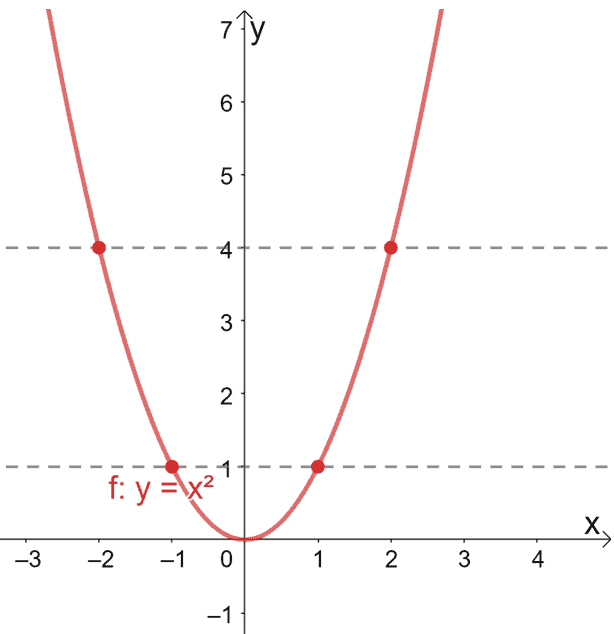
Example 13 Define Function Y F X X 2 Complete The Table



2
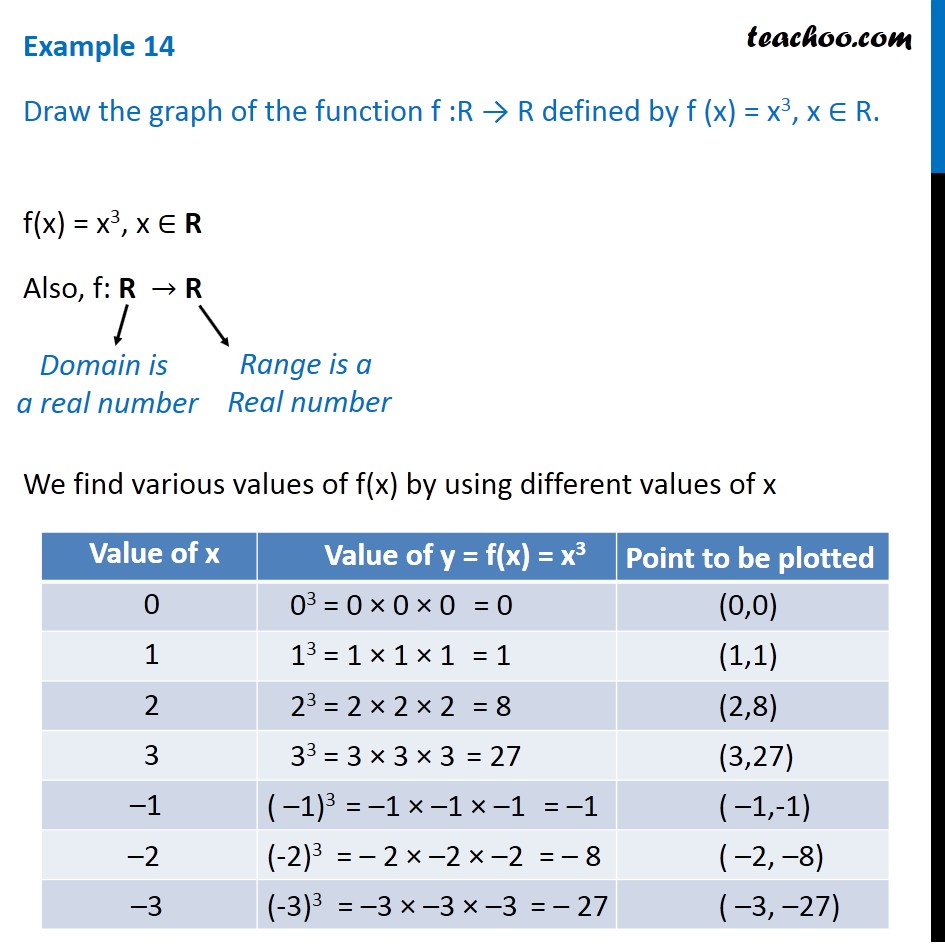



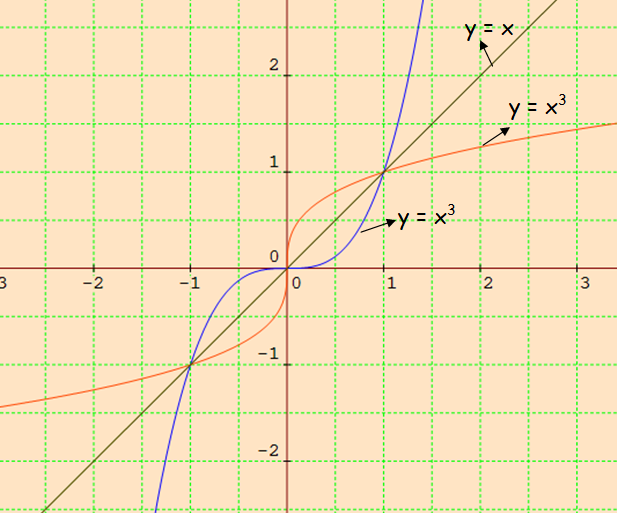
Example 14 Draw Graph Of F X X 3 Chapter 2 Class 11




Function Transformations



How Many Horizontal Asymptotes Can The Graph Of Y F X Have Socratic



One To One Function Explanation Examples



Graph The Function Using Transformations Examples



Solution How Would F 1 Look On A Graph




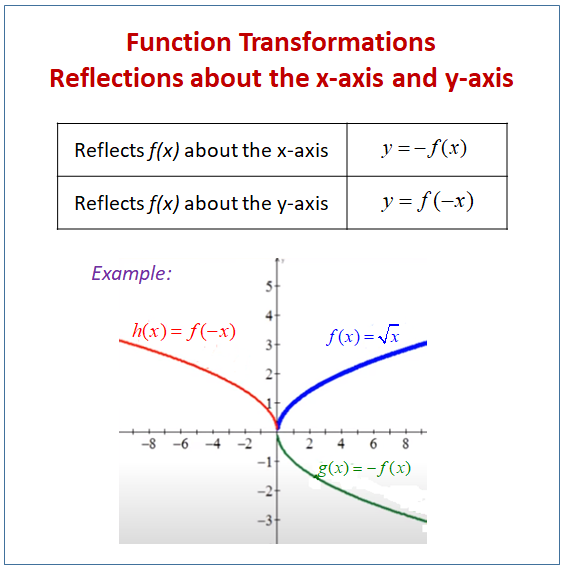
How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




Draw Graph Of Frac 1 F X From Graph Of F X Mathematics Stack Exchange
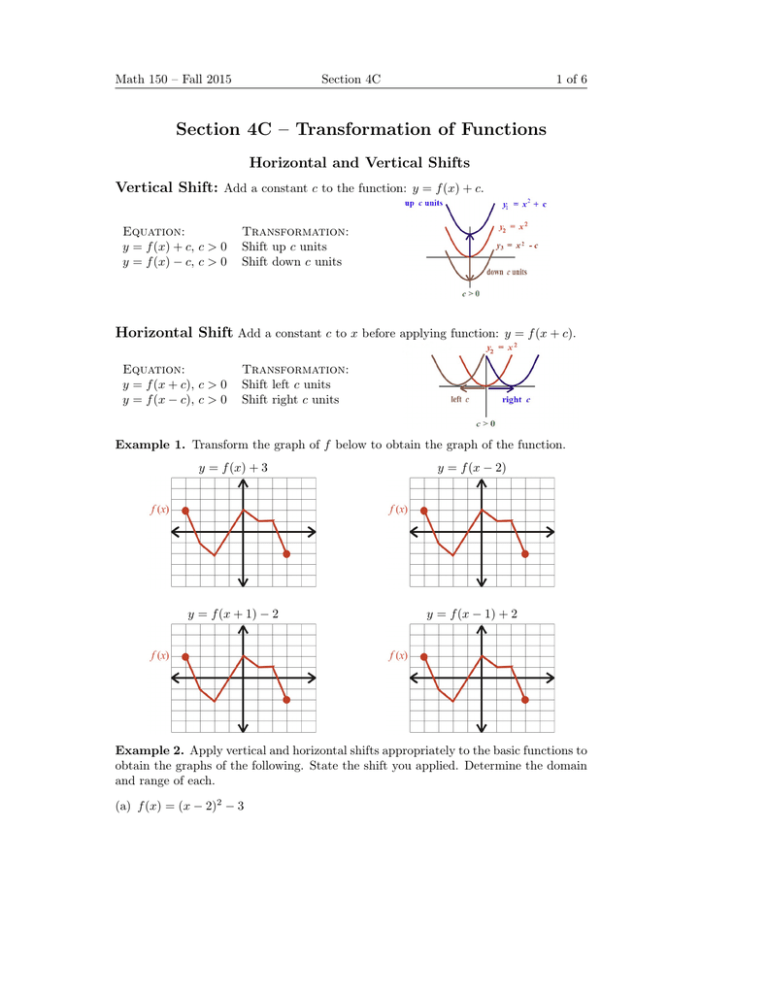



Section 4c Transformation Of Functions Horizontal And Vertical Shifts Vertical Shift



Sat Math Graph Example 2 Sat Math Forbest Academy



Www Pvamu Edu Universitycollege Wp Content Uploads Sites 71 Capeb Pdf
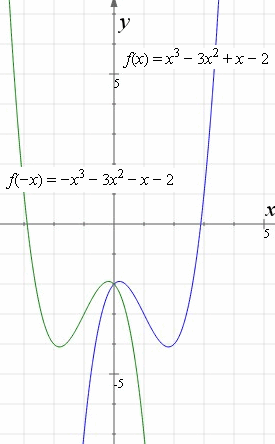



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics



Linear Functions And Their Graphs



Shifting Of Graphs Transformation Example 1 Y F X Kup K Units Y F X Kdown K Units Vertical Shifting Below Is The Graph Of A Function Y Ppt Download




Classpad Graph Example




1 Point A The Graph Of A Function Y F X Is Shifted Up 2 Units Find Homeworklib




1 7 Transformations Mathematics Libretexts



Http Firrhillhigh Org Wp Content Uploads 18 08 Chapter 4 Graphs Of Functions Notes Pdf



Transformations Mrs F X



1 1
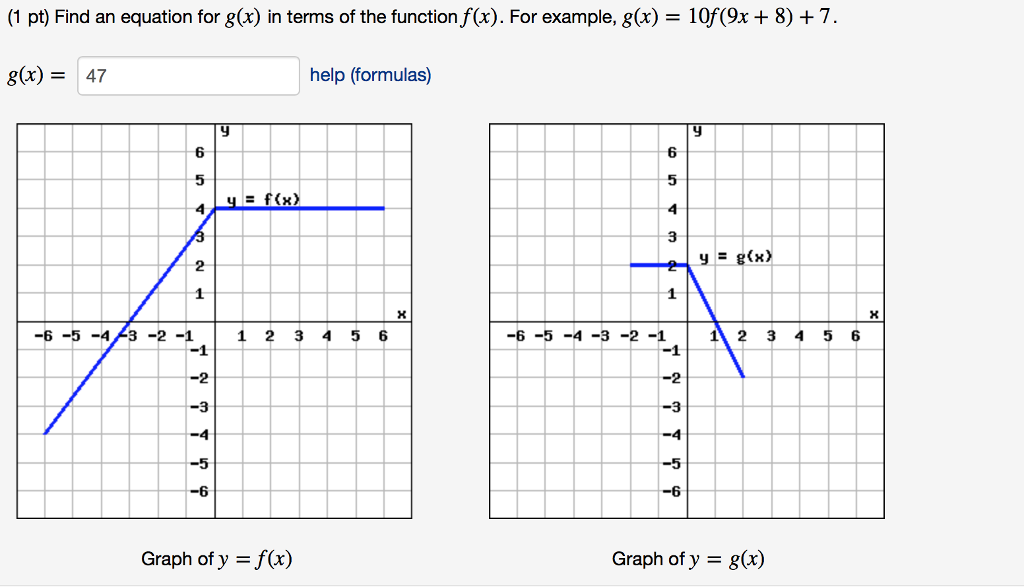



Find An Equation For G X In Terms Of The Function Chegg Com




Transformation Of Graphs I Definition Examples Diagrams
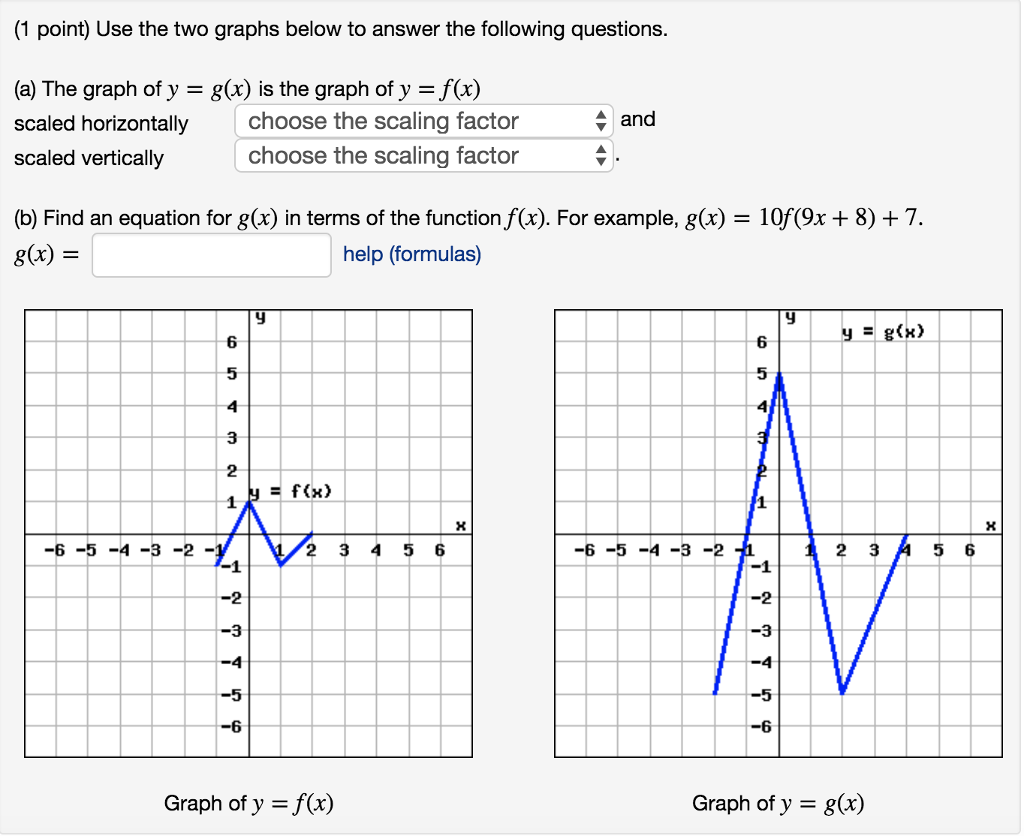



1 Point Use The Two Graphs Below To Answer The Chegg Com




Below Is The Graph Of Y F X Graph Y F X Brainly Com



2




What Is The Difference Between Y F X And Y F X Quora




Graph Of Y X And Y F X In Example 9 Download Scientific Diagram




Translations Of Graphs Iitutor




Linear Functions And Their Graphs



F X F X 2 F X 2
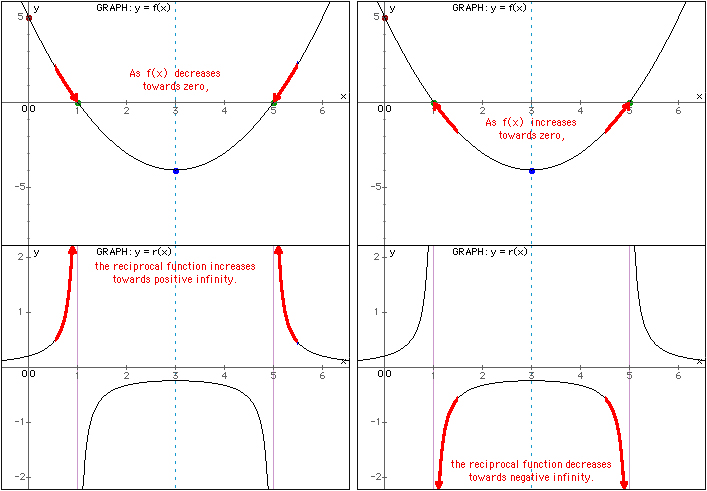



Asymptote



Introduction To Limits In Calculus




Graphs And Level Curves



Business Calculus




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation



Graphing Y F X Examsolutions
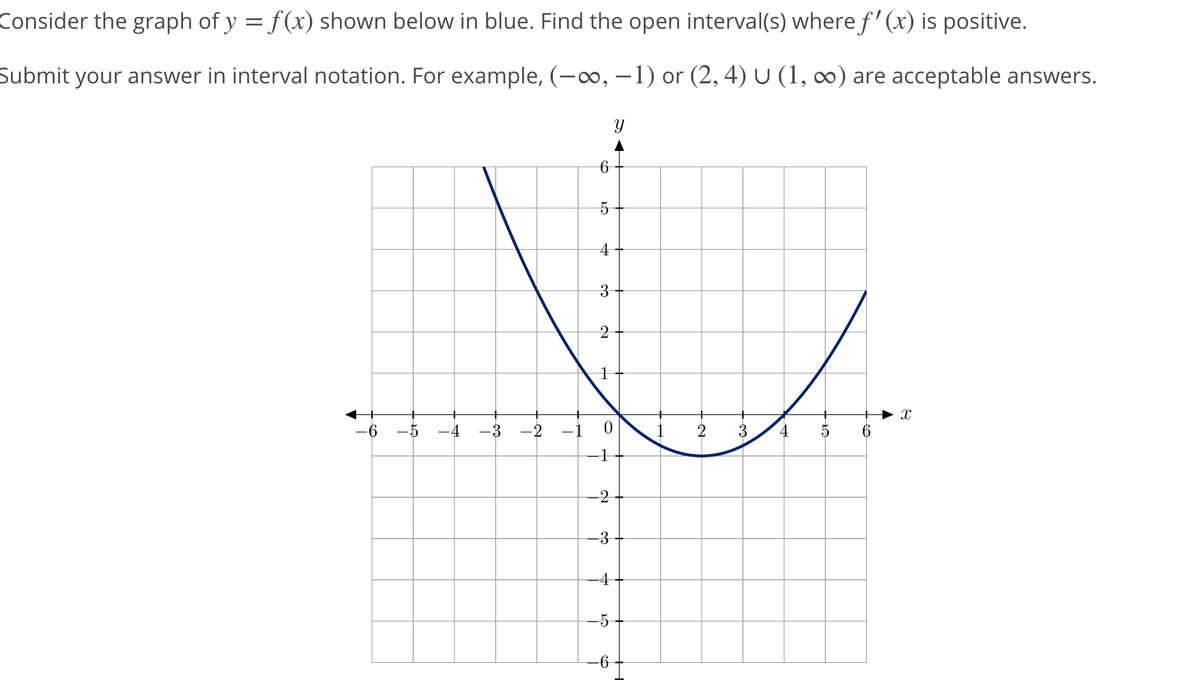



Answered Consider The Graph Of Y F X Shown Bartleby
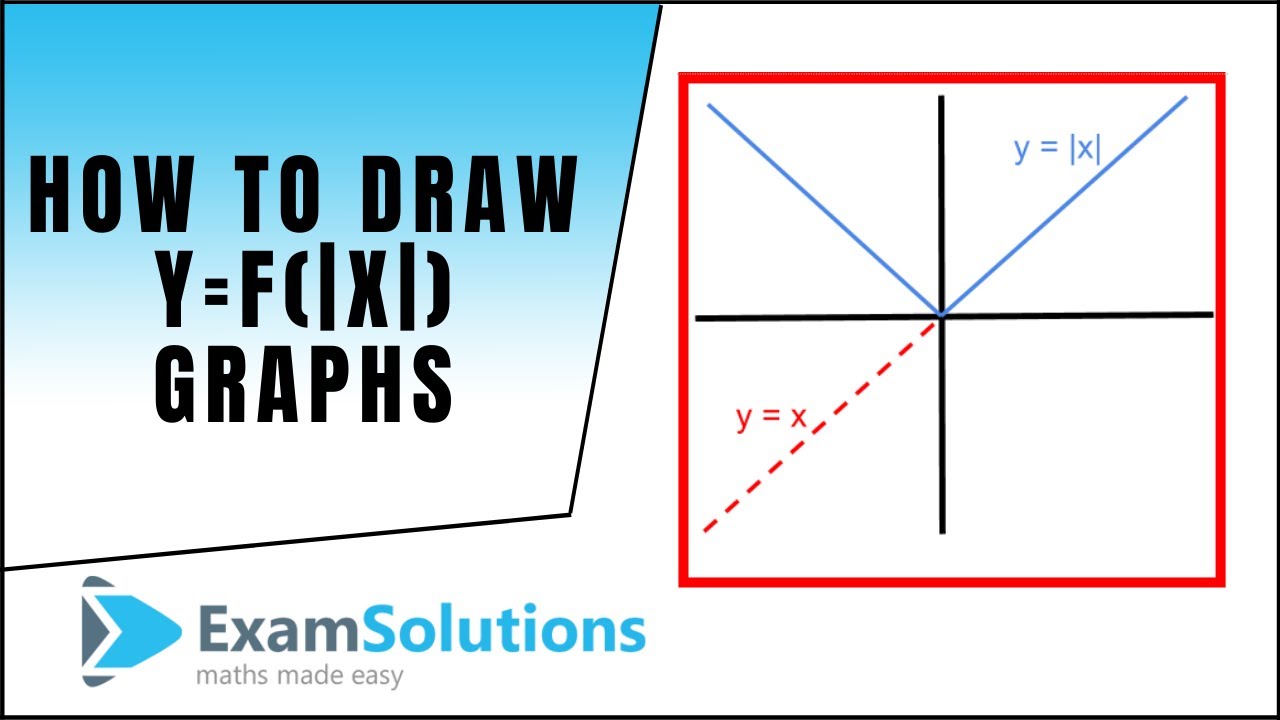



Graphing Y F X Examsolutions




Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help
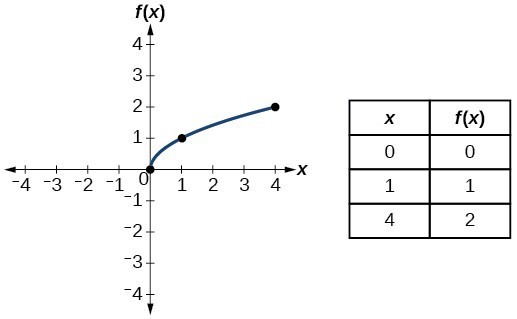



Identify Functions Using Graphs College Algebra



2




Graphing Functions Free Sat Training



Math Scene Derivatives Lesson 2 Differentiating Polynomials



Reflecting Graphs
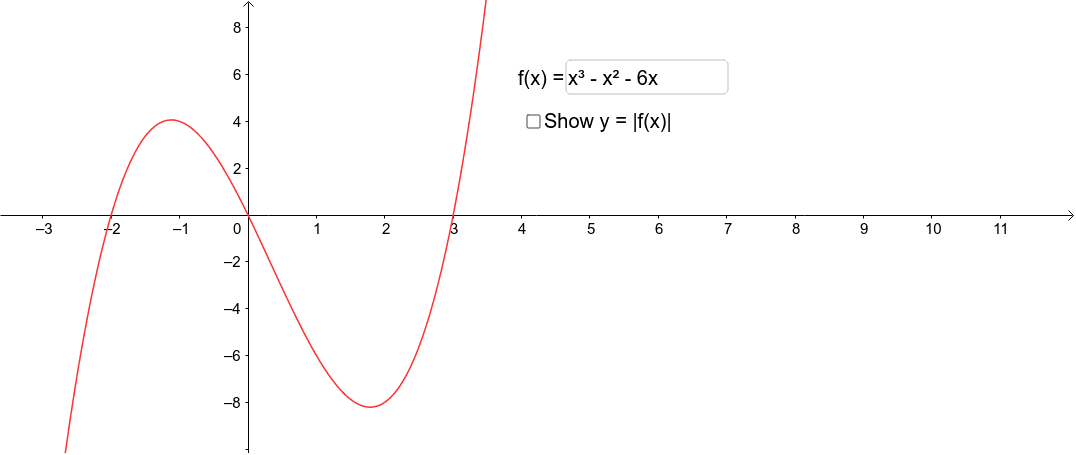



The Graph Of Y F X Geogebra



Search Q Domain And Range Tbm Isch




Example Of Area Bounded By Graph Y F X And Limits X A X B And Download Scientific Diagram




What Is The Difference Between Y F X And Y F X Quora



Solved The Point 4 4 Is On The Graph Of Y 6f X 5 4 What Is The Original Point On Y F X Sketch An Example Of A Relation Which Satis Course Hero
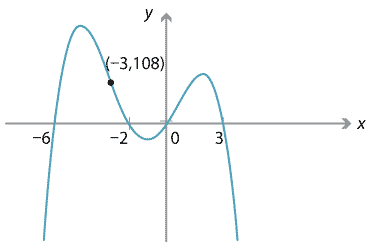



Content Polynomials From Graphs




Transforming Exponential Graphs Example 2 Mathematics Iii High School Math Khan Academy Youtube
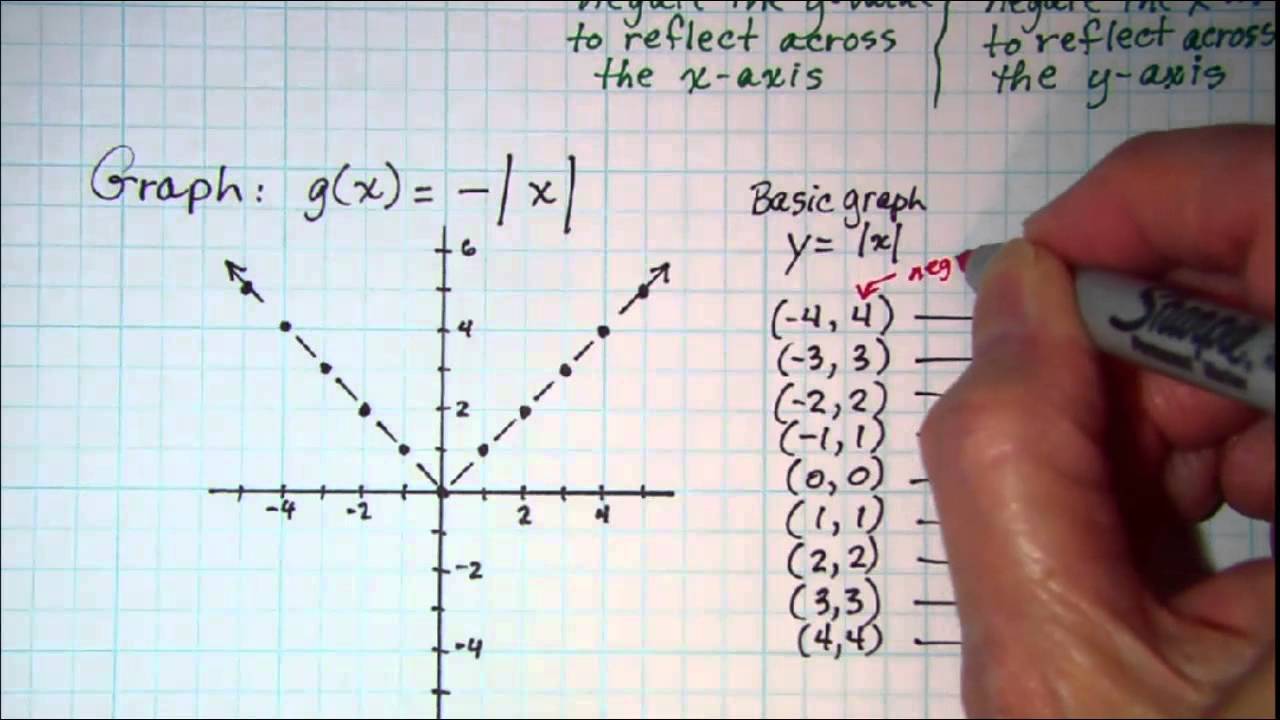



Graphing Reflections Y F X Or Y F X Youtube




Transformations Of Graphs Pdf Free Download
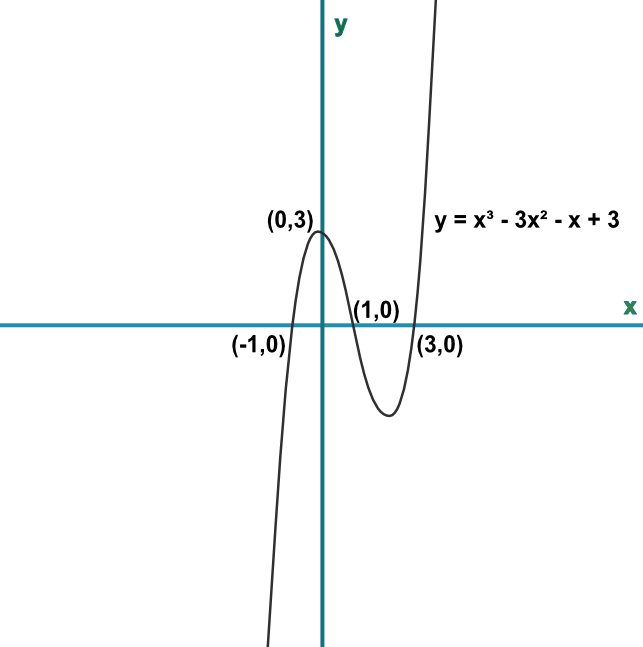



Graphing Cubic Functions
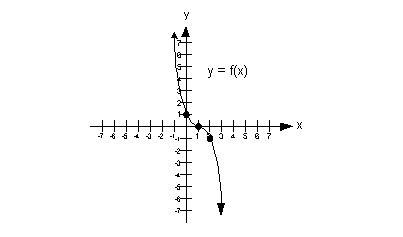



Use The Graph To Determine If The Function Is Even Odd Or Neither
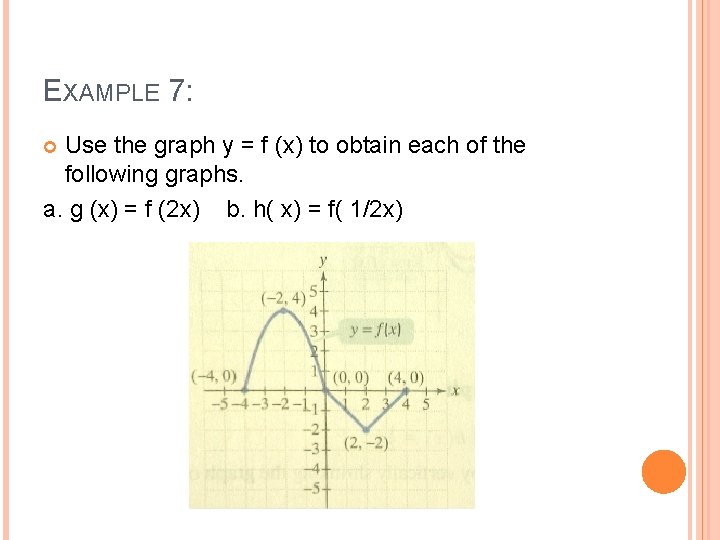



Functions And Graphs Aim 1 2 What Are




Graphing Reflecting Functions Study Com
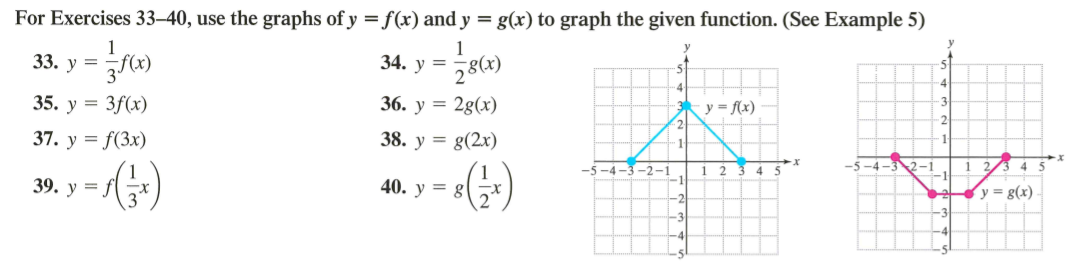



For Exercises 33 40 Use The Graphs Of Y F X And Y Chegg Com



Www Math Utah Edu Wortman 1050 Text If Pdf




Common Functions Reference



Reflecting Functions Or Graphs Examples Solutions Worksheets Videos Games Activities



Y F X Graph Calculator




The Characteristics Of The Graph Of A Reciprocal Function Graphs And Functions And Simultaneous Equations



Squishy Function Graphs



1



1



Graphs Of Y F X And Y F X Geogebra



Www Pearson Com Content Dam One Dot Com One Dot Com Uk Documents Subjects Mathematics Worksheets Chapter4 Example 11 Chapter 4 Translating Reciprocal Graphs Pdf



Worked Examples
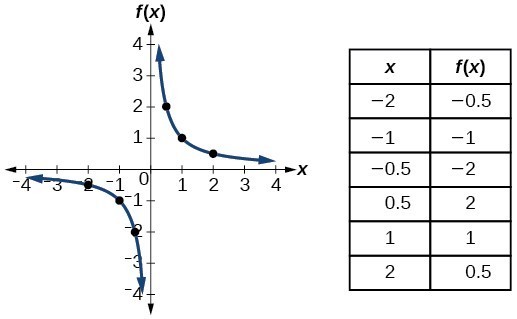



Identify Functions Using Graphs College Algebra
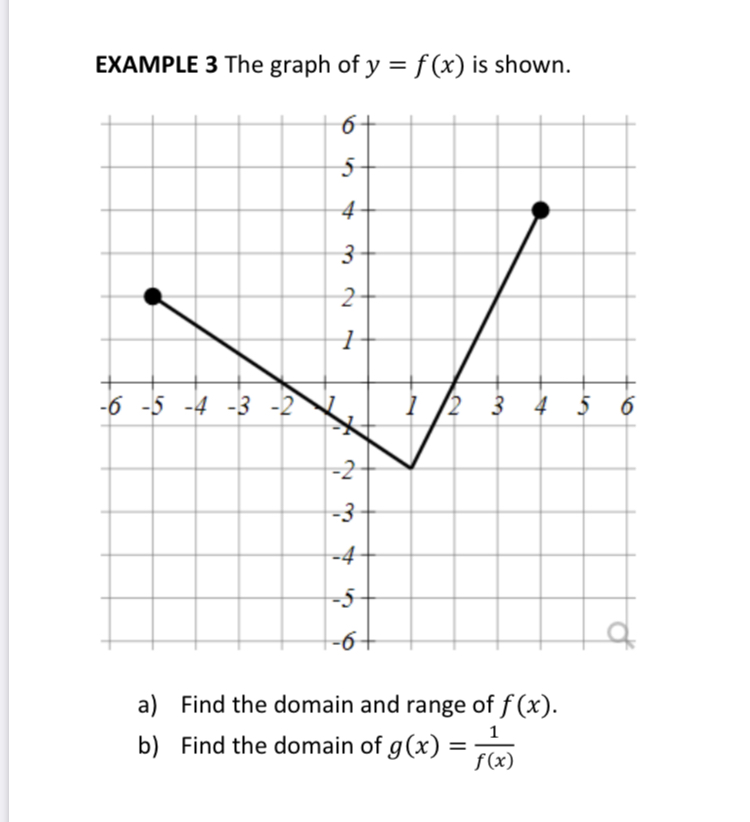



Answered Example 3 The Graph Of Y F X Is Bartleby




Graphs And Transformations Function Mathematics Cartesian Coordinate System
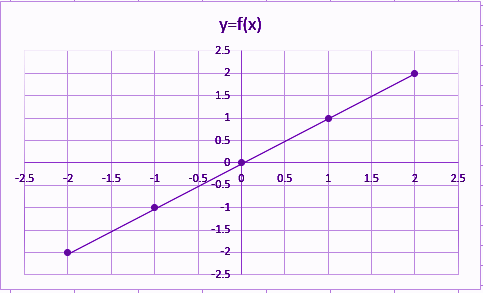



Identity Function Definition Graph Examples
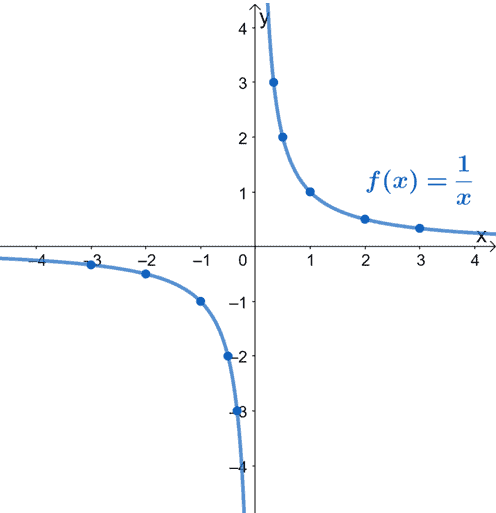



Reciprocal Function Properties Graph And Examples
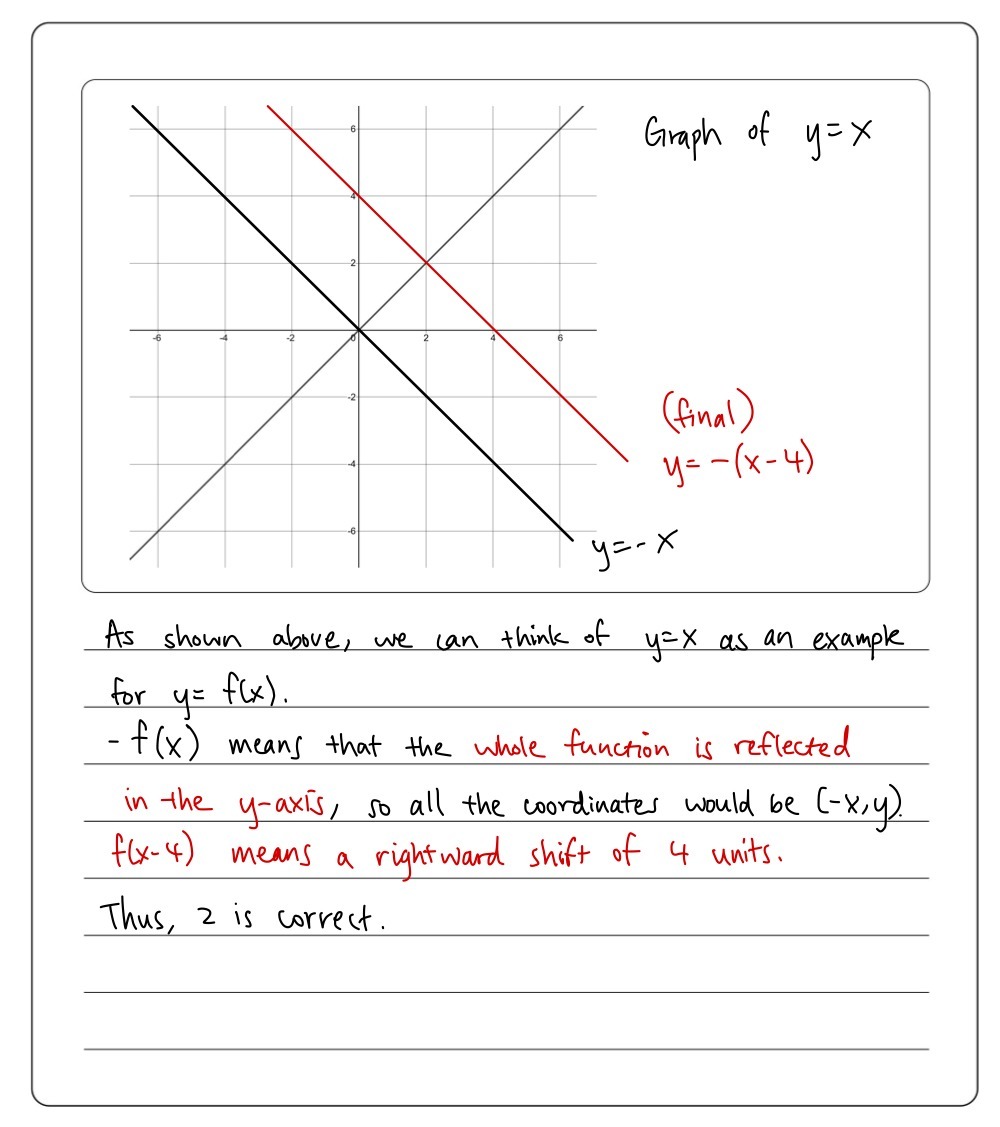



Question 5 1 Point 5 If The Function Y Fx 4 We Gauthmath



0 件のコメント:
コメントを投稿