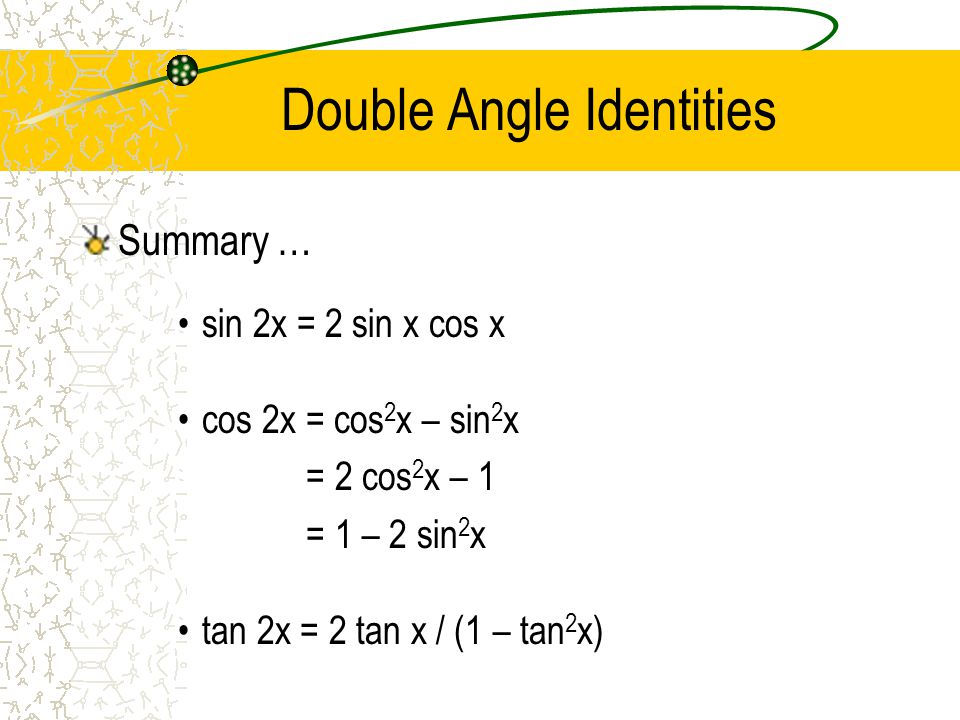
Sec2(2x) sec 2 ( 2 x) Because the two sides have been shown to be equivalent, the equation is an identity tan2(2x)sin2(2x) cos2(2x) = sec2 (2x) tan 2 ( 2 x) sin 2 ( 2 x) cos 2 ( 2 x) = sec 2 ( 2 xSin 2x = 2 sin x cos x • Cosine cos 2x = cos2 x – sin2 x = 1 – 2 sin2 x = 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;Answer (1 of 6) Verify the following identity sin(x)^2 cos(x)^2 tan(x)^2 = 1/cos(x)^2 Hint Eliminate the denominator on the right hand side Multiply both sides by cos(x)^2 cos(x)^2 (cos(x)^2 sin(x)^2 tan(x)^2) = ^?1 Hint Express the left hand side in terms of sine and cosin
3
Sin 2x cos 2x tan 2x
Sin 2x cos 2x tan 2x-Integral of sin^2x*cos^2x, Double angle identity & power reduction, https//youtube/6XmbiKGCK14integral of cos^2(x), https//youtube/Kq8hU80xDPM ,integral ctg² 1 = csc² x sin 2x = 2 sin x cos x cos 2x = cos² x sin² x = 2 cos² x 1 = 1 2 sin² x tan 2x = (2 tan x) / (1 tan² x) sin 3x = 3 sin x 4 sin³ x cos 3x = 4 cos³ x 3 cos x tan 3x = (3 tan x tan³ x)/ (1 3 tan² x) 1 cos x = 2 sin² ½x 1 cos x = 2 cos² ½x
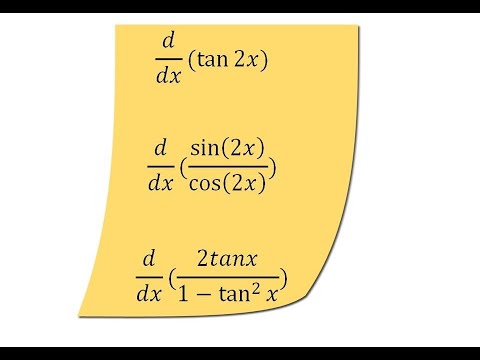



Derivative Of Tan2x Sin2x Cos2x And 2tanx 1 Tan 2x Youtube
Ex 72, 39∫1 𝑑𝑥/(𝑠𝑖𝑛2 𝑥 𝑐𝑜𝑠2 𝑥) equalstan x cot x C (B) tan x – cot x C tan x cot x C (D) tan x – cot 2x C ∫1 〖" " 𝑑𝑥/(sin^2 𝑥 cos^2𝑥 )〗= ∫1 〖" " 𝟏/(sin^2 𝑥 cos^2𝑥 ) 𝑑𝑥〗 = ∫1 〖" " (〖𝐬𝐢𝐧〗^𝟐 𝒙 〖 〖𝐜𝐨𝐬〗^𝟐〗𝒙)/(sin^2 𝑥 cos^2𝑥 ) 𝑑𝑥〗 = ∫ My son asked for help with his maths homework last night The question was to show that $$\tan (2x) = 5\sin(2x)$$ can be written as $$\sin(2x)(15\cos(2x))=0$$ My first response was to rearrange as $\tan (2x) 5\sin(2x) = 0$, replace $\tan$ with $\frac{\sin}{\cos}$ and multiply through by $\cos$, etcThis worked fine He then told me that he'd started by dividing by $\tan Get an answer for 'Prove that tan^2x/(1tan^2x) = sin^2x' and find homework help for other Math questions at eNotes
Cosine 2X or Cos 2X is also, one such trigonometrical formula, also known as double angle formula, as it has a double angle in it Because of this, it is being driven by the expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions Let us start with the cos two thetas or cos 2X or cosine Therefore, the values of sin(2X), cos(2X) and tan(2X) are – √35 / 18, 17 / 18 and – √35 / 17 respectively Similar Questions Question 1 Find sin(2X),cos(2X) and tan(2X) from given information secX = 8, X lies in Quadrant IVSimple and best practice solution for sin(2x30)=cos(2x30) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework
Answer (1 of 12) Since, cos2x=cos^{2}xsin^{2}x 1cos2x=1(cos^{2}xsin^{2}x) 1cos2x=1cos^{2}xsin^{2}x We know, sin^{2}xcos^{2}x=1 Therefore, sin^{2}x=1cos^{2}xAnswer (1 of 7) If sin(x) = 12/(13), cos(x) = 5/(13) and tan(x) = 12/5 sin(2x) = 2sin(x)cos(x) = (2)(12)(5)/(13^2) = (1)/(169) cos(2x) = √(1 sin^2(2x{eq}\displaystyle (\cot^2x \sin^2x) (\tan^2 x \cos^2x) {/eq} Quotient Identities In trigonometry, there are a couple of quotient identities They are defined by two trigonometric functions
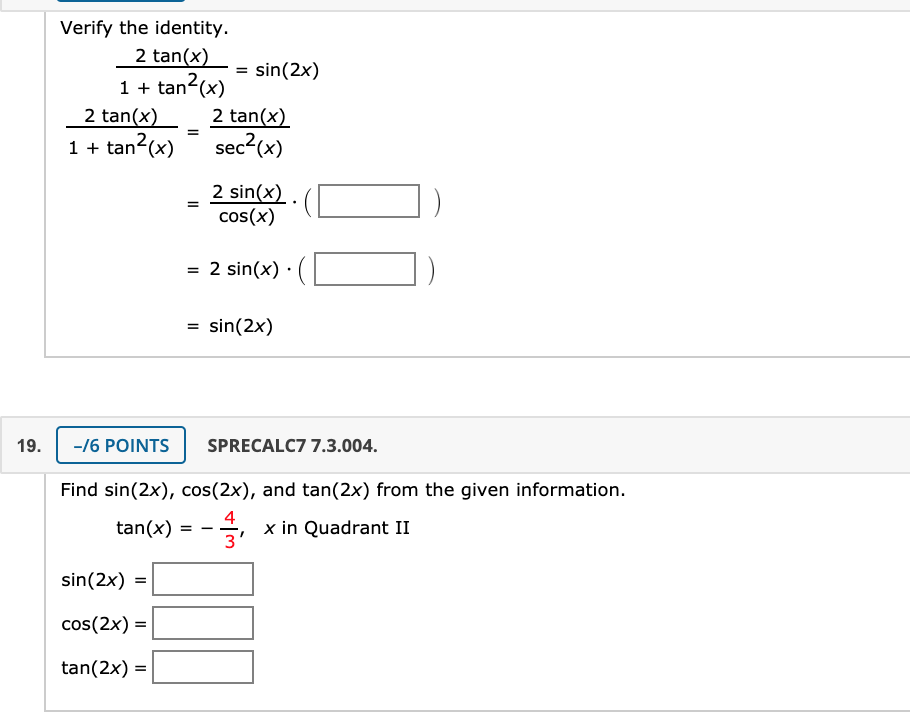



Solved Verify The Identity 2 Tan X Sin 2x 1 Tan X Chegg Com
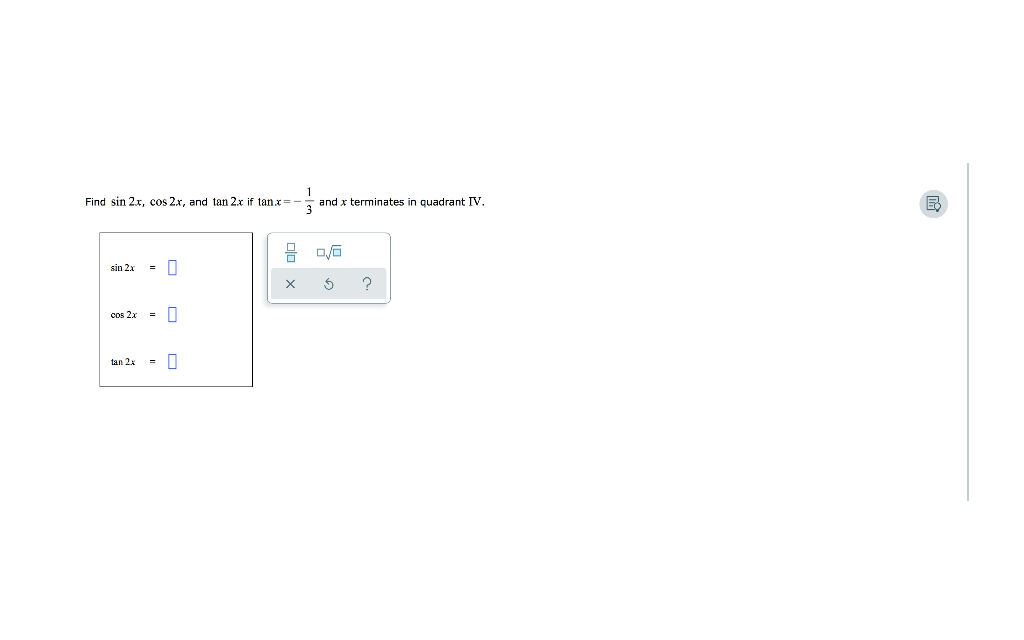



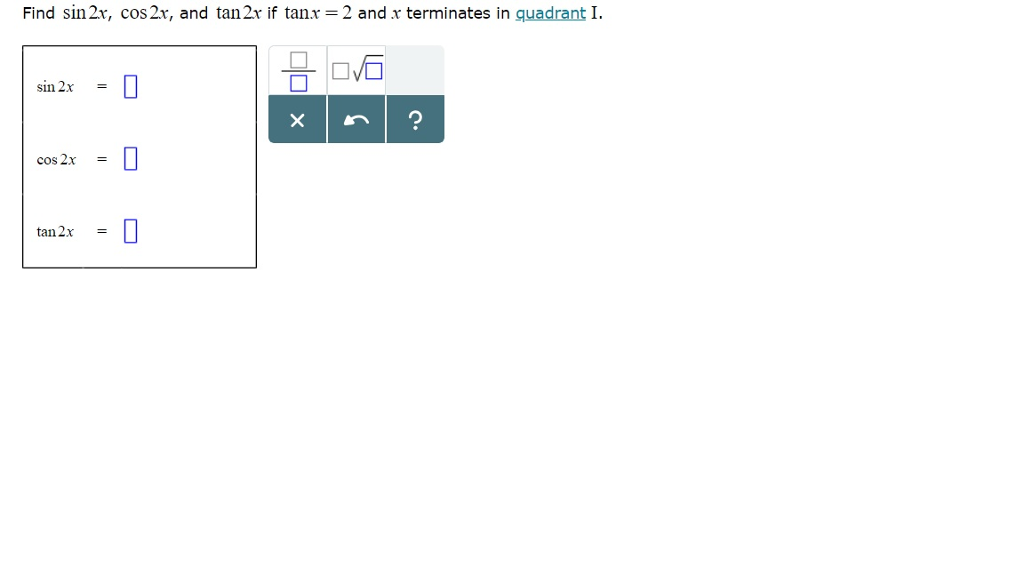
Solved Find Sin 2x Cos 2x And Tan 2x If Tanx And X Chegg Com
How to find the value of sin 2x cos 2x?Answer (1 of 6) cos3x = cos(2xx) cos(2xx)= cos2xcosxsin2xsinx =(2cos^2x1)cosx 2sinxcosx(sinx) =2cos^3xcosx 2sin^2xcosx =2cos^3xcosx 2(1cos^2x)cosx =2cos^3xcosx 2cosx2cos^3x 4cos^3x 3cosx Get an answer for 'Evaluate the integral of function y=cos2x/cos^2x*sin^2x' and find homework help for other Math questions at eNotes




Answered 15 Find Sin 2x Cos 2x And Tan 2x If Bartleby



3
sin^2xsin^2xtan^2x=tan^2x Simplify sin^2xsin^2xtan^2x First, factor out sin^2x from the expression sin^2x(1tan^2x) Now we can use this trig identity 1tan^2x=sec^2x Now we have sin^2xsec^2x We know that secx=1/cosx So it is then true that sec^2x=1/cos^2x Now we have sin^2x/cos^2x We know that tanx=sinx/cosx So it is then true that tan^2x=sin^2x/cos^2x So forAnswer (1 of 2) Remember Cos(A B) = CosACosB SinASinB Now instead of B it is A Cos(A B) = CosACosB SinASinB Cos(A A) = CosACosA SinASinA A A can be simplified to 2A and CosA*CosA can become Cos^2A and the same for Sin Cos(2A) = Cos^2A Sin^2AExperts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high 100% (10 ratings) Transcribed image text Prove the identity 1 cos (2x)/sin (2x) = tan (x) 1 cos (2x)/sin (2x) = 1 (1 2sin^2 (x))/2 sin (x) () = 2 ()^2/2sin (x)cos (x) = tan (x)



Piu Veloce Sin2x Cos2x 1




How Do You Prove Sec 2x Tan 2x Cos 2x Sin 2x Socratic
Tan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 ) cos x cos y = 2 sin ( (x y)/2 ) sin ( (x y)/2 ) Trig Table of Common Angles angle\sin 2x\cos 2x=1 2\sin x\cos x\cos^2x\sin^2x\sin^2x\cos^2x=0 2\sin x\cos x2\cos^2x=0 \cos x(\sin x\cos x)=0 \cos x=0\Rightarrow x=\frac{\pi}{2}k\pi,\tan x=1/x2 sin xdx = x2 cos x 2x x 2cos x C x2 cos x x2sinx2xcosx 2x sin x 2xcosx 2sinx 2cos x 2sin x This more contemplative scheme seems more informative than the other you can see the mechanism, the work is very easy to check, and the final answer is very easy to read off




Prove The Identity 1 Tan 2x 1 Tan 2x 1 2sin 2x In Urdu Hindi Youtube
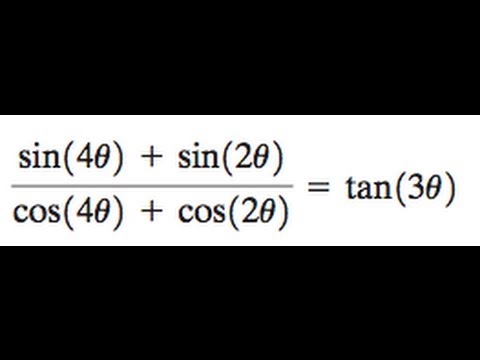



Solve Sin 4x Sin 2x Cos 4x Cos 2x Tan 3x Youtube
Expert Answer Who are the experts?Thus, the value of cos2x = 17 25 cos 2 x = 17 25 Now, the value of tan2x tan 2 x is computed as shown below, tan2x= sin2x cos2x Standard Relation = 4√21 25 17 25 SubstituteConvert from 1 cos(2x) 1 cos ( 2 x) to sec(2x) sec ( 2 x) Replace the expressions with an equivalent expression using the fundamental identities Multiply tan(2x) tan ( 2 x) by 1 1 Factor tan(2x) tan ( 2 x) out of sec(2x)tan(2x)− tan(2x) sec ( 2 x) tan ( 2 x) tan ( 2 x) Tap for more steps




Answered Find Sin2x Cos2x And Tan2x If Bartleby
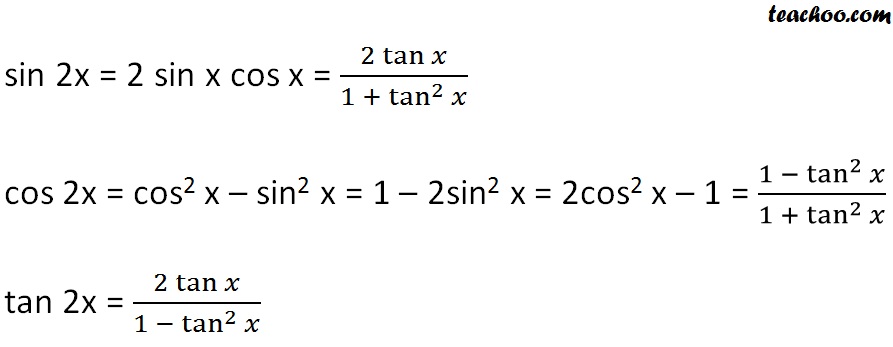



上 Tan2x Identity ただの悪魔の画像
Free trigonometric identities list trigonometric identities by request stepbystepThis video explains the proof of all the three fundamental identities of Trigonometry ie sin^2xcos^2x=1, 1tan^2x=sec^2x and 1cot^2x=csc^2x using PythagoClick here👆to get an answer to your question ️ If 5(tan^2x cos^2x) = 2cos 2x 9 , then the value of cos 4x is




Integrate Sec 2x Method 2



Solved Verify The Identity 2tan X Sin 2x 1 Tan2 X 2 Chegg Com
(sin^2x tanx)/(cos^2x cotx) = tan^2(x)Raise cos ( 2 x) cos ( 2 x) to the power of 1 1 Use the power rule a m a n = a m n a m a n = a m n to combine exponents Add 1 1 and 1 1 Cancel the common factor of cos ( 2 x) cos ( 2 x) Tap for more steps Move the leading negative in − sin ( 2 x) cos ( 2 x) sin ( 2 x) cos ( 2 x to prove #cot^2xcos^2x=cot^2xcos^2x# take LHS and change to cosines an sines and then rearrange to arrive at the RHS #=cos^2x/sin^2xcos^2x# #=(cos^2xcos^2xsin^2x)/sin^2x#




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube




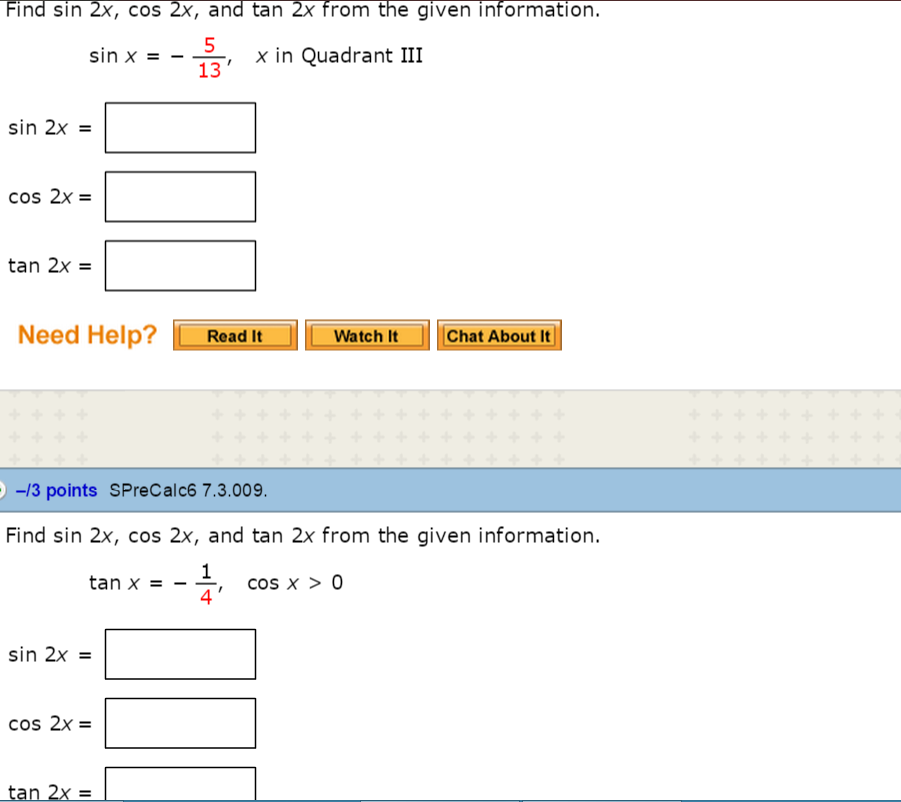
View Question Find Sin 2x Cos 2x And Tan 2x From The Given Information Tan X 1 2 Cos X 0
Question Decide whether the equation is a trigonometric identiye explain your reasoning cos^2x(1tan^2x)=1 secxtanx(1sin^2x)=sinx cos^2(2x)sin^2=0 Best answer The given integral is ∫ tan–1 (sin 2x/ (1 cos2x)) dx = ∫ tan–1 (2sin x cos x/ (2cos2 x)) dx = ∫ tan–1 (tan x) dx = ∫ x dx = (x2/2) c Please log in or register to add a comment ← Prev Question Next Question →Prove that `(1 sin 2x cos 2x)/(1 sin 2x cos 2x) =tan x`




Cos 2x Formula Derivation Examples What Is Cos 2a Formula



What Is Integral Of Sin2x Tan2x Quora
Simplify sin(2x)tan(x)cos(2x) Simplify terms Tap for more steps Simplify each term Tap for more steps Rewrite in terms of sines and cosines Combine and Simplify the numerator Tap for more steps Apply the sine doubleangle identity Combine exponents Tap for more steps Raise to the power of Raise to the power of Use theFree trigonometric equation calculator solve trigonometric equations stepbystepIntegrating Al and Bl wrt x, We have A — sin 2x— log ( sec 2x tan 2N )CI B — cos2x Hence complete solution is y— cos 2x c2 sin2x — cos 2x log (sec 2x tan 2x) Ans EM52 Q14 Solve d2y dy 3 v2 dv BTech (11 serm) Hence the given equation is not exact therefore to use an integration factor here to change the given' h into



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com
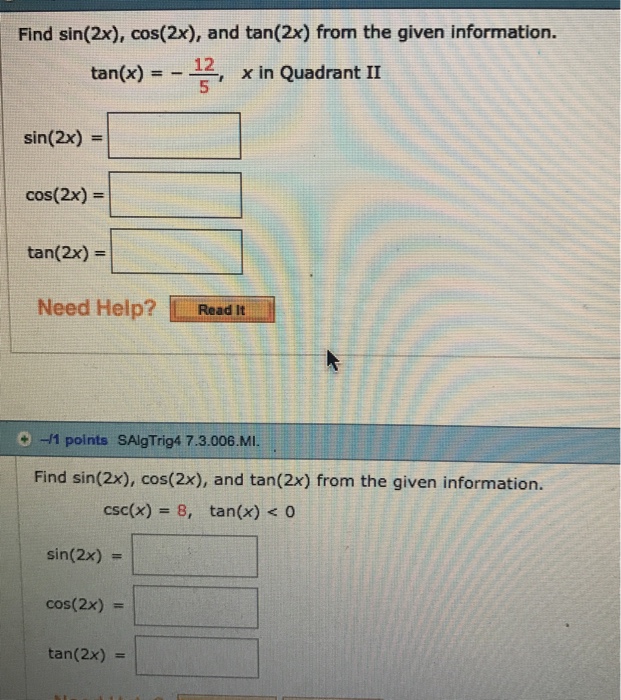
Answer to Find sin 2x, cos 2x, and tan 2x if cos x = 4 / 5 and x terminates in quadrant II By signing up, you'll get thousands of stepbystepIn other words, cosθ is the adjacent side divided by the hypotenuse We make use of the trigonometry double angle formulas, to derive this identity We want to find the value of sin 2x cos 2x To do this, multiply equation (i) and (ii) Cancel out cos 2x Cancel out cos 2xMath Trigonometry Trigonometry questions and answers 2 Find sin 2x, cos2x, and tan 2x if tanx and x terminates in quadrant II 3 DO 0/6 sin 2x x 5 ?



1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit




Trigonometric Identity Sinx Sin2x 1 Cosx Cos2x Tanx With Double Angle Expressions Youtube
= (1 tan 2 x)/(1 tan 2 x) Because tan x = sin x / cos x Hence, we have cos 2x = (1 tan 2 x)/(1 tan 2 x) in terms of tan xTan^2xsin^2x = tan^2xsin^2x start with left side tan^2xsin^2x =(sin^2x/cos^2x)sin^2x =(sin^2xsin^2xcos^2x)/cos^2x =sin^2x(1cos^2x)/cos^2x =sin^2x*sin^2x/cos^2x =tan^2xsin^2x verified left side=right sideCos 2x tan 2x



Prove Sin2x 2tanx 1 Tan 2x Socratic



Why Does The Example Not Include Cos2x 0 The Student Room
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor Next, it will be tan x to the power cot x, and in the third brackets, cos x/sinx into cos x/sin x into 1/cos^2x minus log tan x into cosec^2x Now we are canceling the cos x Then dy/dx equals tan x to the power cot x into cosec square x minus cosec square x into log tan x After some calculation, the answer is tan to the power cot x into cosecSinx cosx / (cos^2x sin^2 x) = tanx/(1tan^2x)



Solved Find Sin 2x Cos 2x And Tan 2x If Tanx 2 And X Chegg Com




Trig Graphs Investigate The Effects Of 2sin X 2cos X 2tan X Ppt Video Online Download
A) $\tan ^2x4\cos ^2x7=4\tan x8\cot x$ b) $6\sin ^2x2\cos ^2x2\sqrt{3}\sin 2x=14\sin \left(x\frac{\pi }{6}\right)$ Lớp 11 Toán Bài 4 Ôn tập chương Hàm số lượng giác và phương t2x 3x 4x 5x 6x 7x 8x 9x 10x Speedup over MKL cuBLAS >1 TFLOPS doubleprecision • cuBLAS 50 on KX, input and output data on device • MKL 1036 on Intel SandyBridge EW @ 310GHz 0 500 1000 1500 00 2500 3000 GFLOPS Performance may vary based on OS version and motherboard configuration




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




Vii Tan 17 Sin 4x Solution Let Y Tan 1 1 Sin 4r V1 Sin 4x
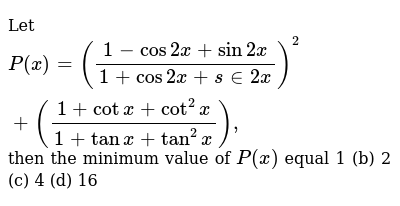



Let P X 1 Cos2x Sin2x 1 Cos2x S In2x 2 1 Cotx Cot 2x 1 Tanx Tan 2x Then The Minimum Value Of P X Equal 1 B 2 C 4 D 16
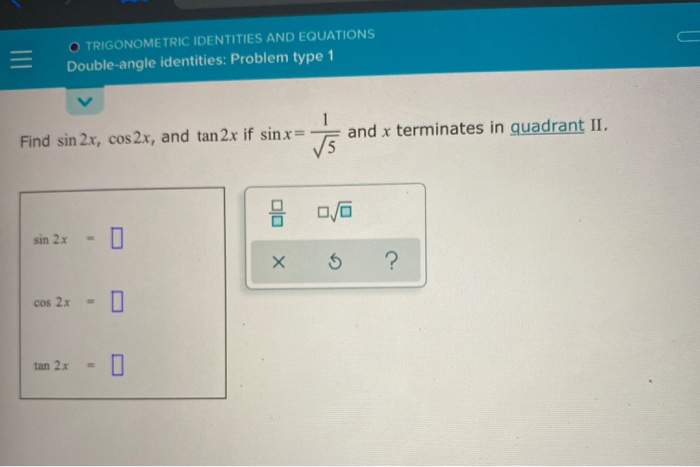



Solved Find Sin2x Cos2x And Tan 2x If Sin X 1 Square Root Chegg Com




15 Find Sin 2x Cos 2x And Tan 2x If Tanx And X Terminates In Homeworklib



Finding Cos 2x Sin 2x And Tan 2x Youtube
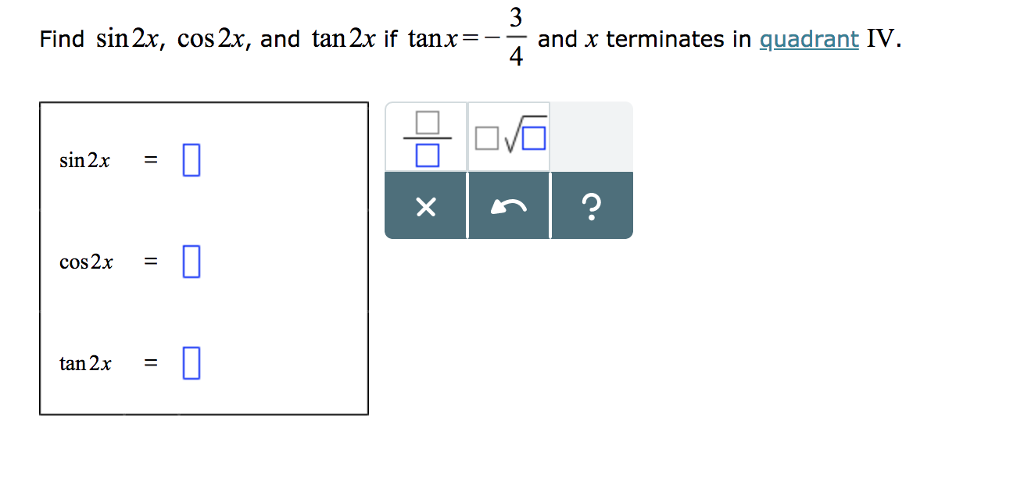



Solved Find Sin2x Cos 2x And Tan 2x If Tanx And X Chegg Com




Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube




Tan2x ただの悪魔の画像



What Is Integral Of Sin2x Tan2x Quora
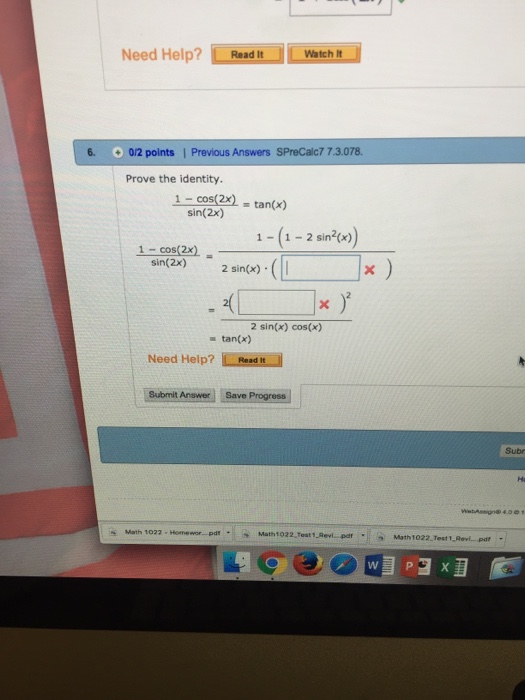



Solved Prove The Identity 1 Cos 2x Sin 2x Tan X 1 Chegg Com



How To Show That 1 Cos2x Sin2x Tanx Youtube




5 5 Multiple Angle And Product Sum Formulas Find All Solutions In Ppt Download




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com



1
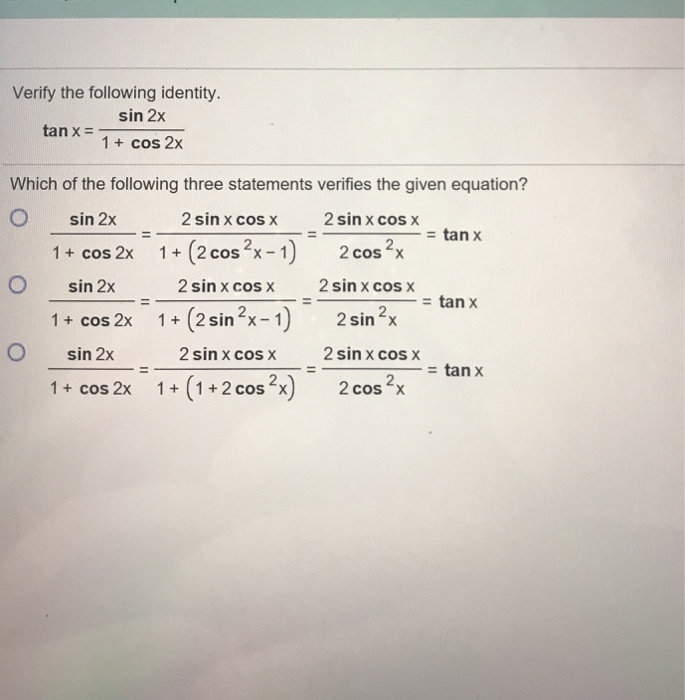



Solved Verify The Following Identity Tan X Sin2x 1 Cos Chegg Com




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Day 3 Hw 3 To 4 Find Sin2x Cos2x And Tan2x Given One Trig Value And The Quadrant Youtube




Find Sin 2x Cos 2x And Tan 2x If Tan X 1 2 And X Terminates In Quadrant Iii Helpyout
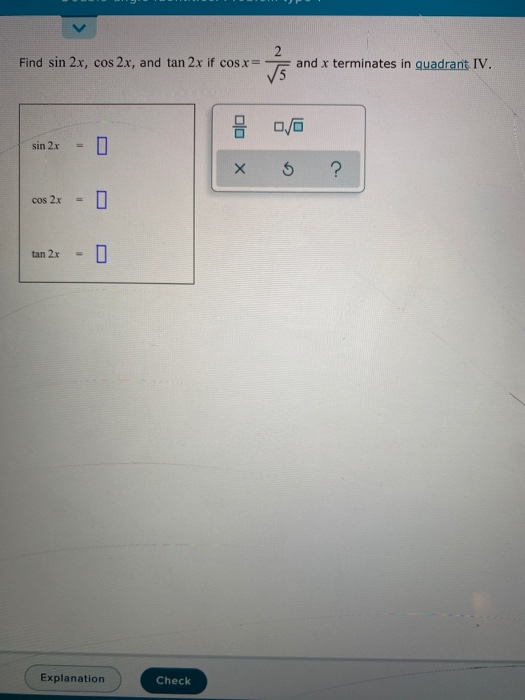



Solved Find Sin2x Cos2x Tan2x If Cosx 2 Root5 And X Chegg Com




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Cos2x 1 Sin2x Tan Pi 4 X Double And Half Angle Identity Youtube



Prove That Cos2x Cos 2x Sin 2x 2cos 2x 1 1 2sin 2x 1 Tan 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community




Find The Value Of Sin 2x Cos 2x And Tan 2x Given One Quadratic Value And The Quadrant Youtube
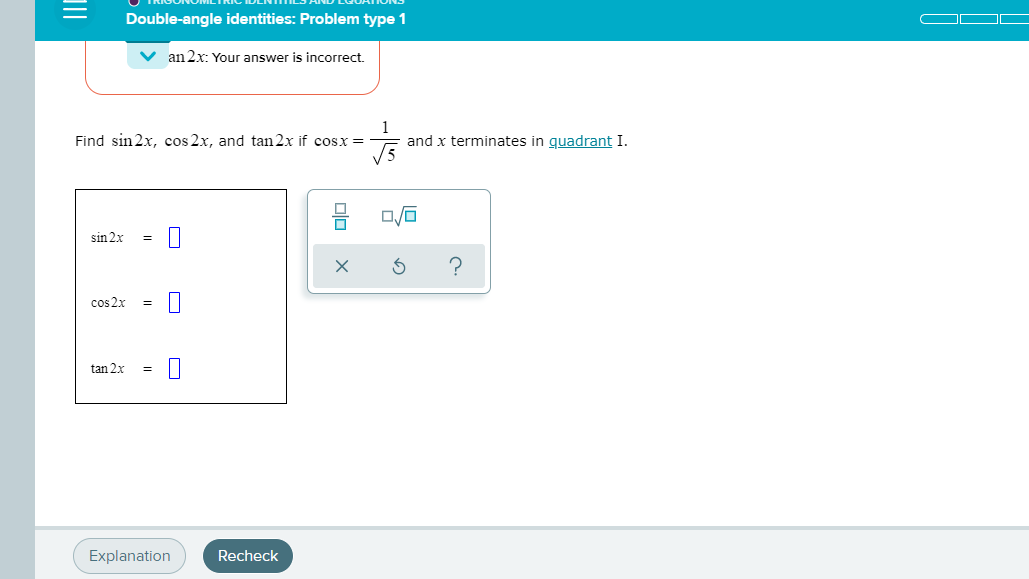



Solved Find Sin2x Cos2x And Tan2x If Cosx 1 Square Root 5 Chegg Com




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified




If Sin2x Cos2x Tan2x Cot2x Sec2x Cosec2x 7 Then Value Of Sin2x Is Maths Meritnation Com
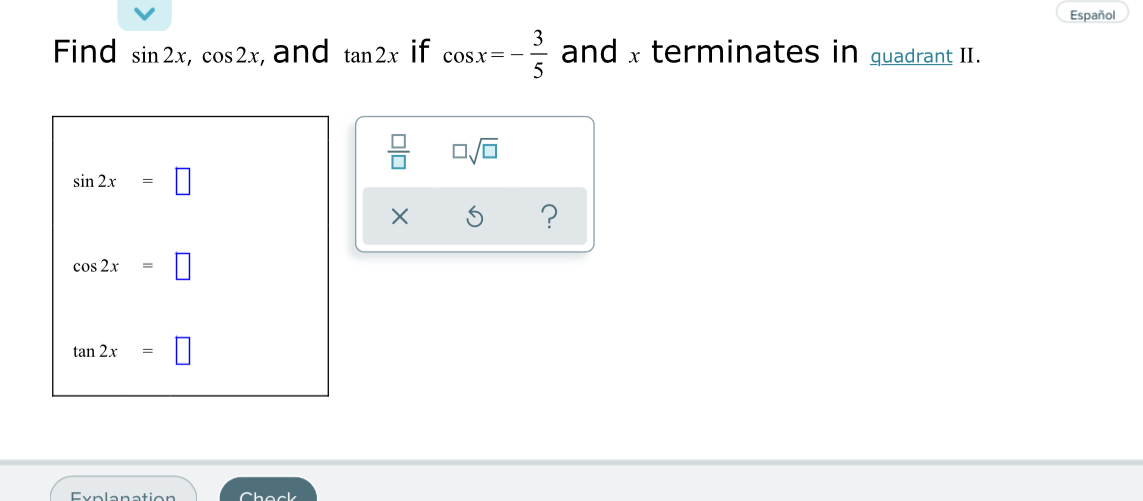



Answered 3 Find Sin 2x Cos 2x And Tan 2x If Bartleby
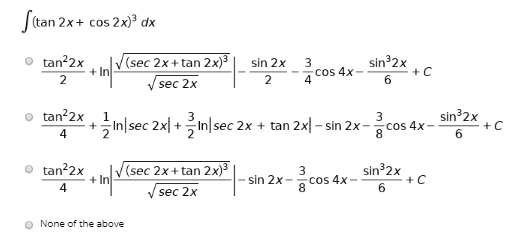



Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby




Answered Prove The Identity Sin 2x 1 Cos 2x Bartleby



What S The Minimum Value Of Math Sin 2x Cos 2 X Tan 2x Sec 2x Cosec 2x Cot 2x Math Why Can T We Use Am Gm Inequality Quora
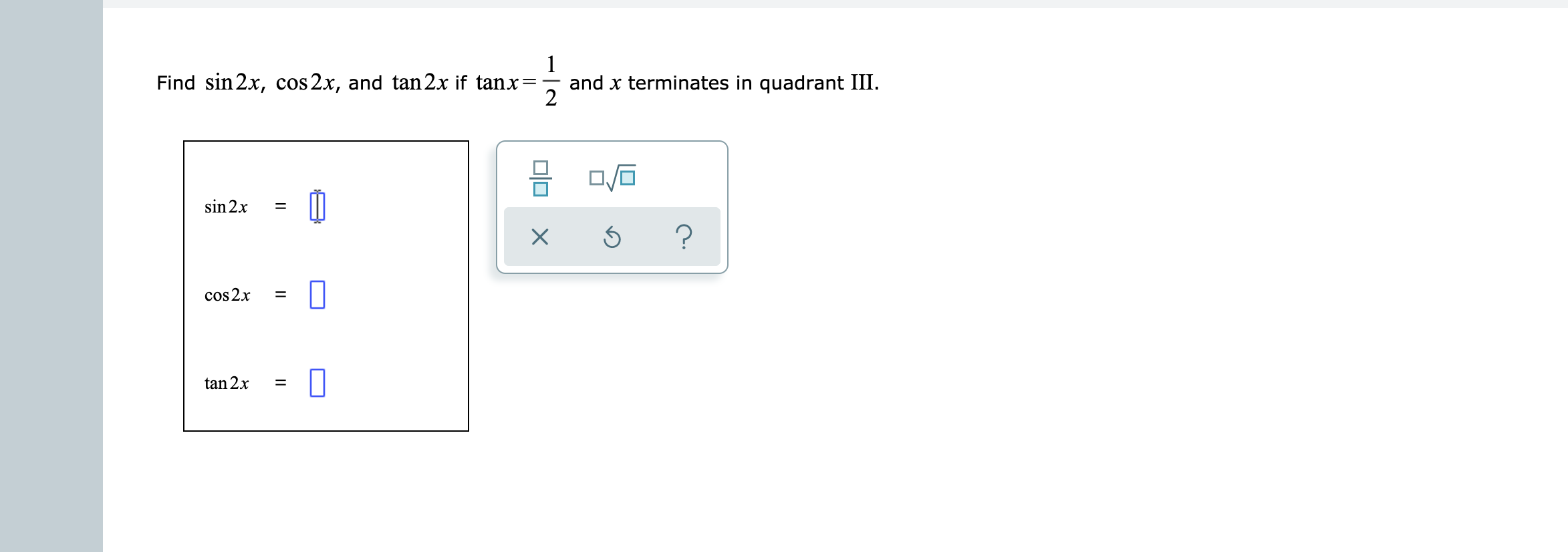



Answered 1 Find Sin 2x Cos 2x And Tan 2x If Bartleby




Sin 2x Cos 2x Tan 2x In Terms Of Tan X Youtube




Derivative Of Tan2x Sin2x Cos2x And 2tanx 1 Tan 2x Youtube



Prove The Identity Cos 2x 1 Sin 2x Tan P 4 X Sarthaks Econnect Largest Online Education Community




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube




Solve Trigonometric Equation Sec 2 X 5 1 Cos2x 3 Tan 2 Xsin2x Youtube
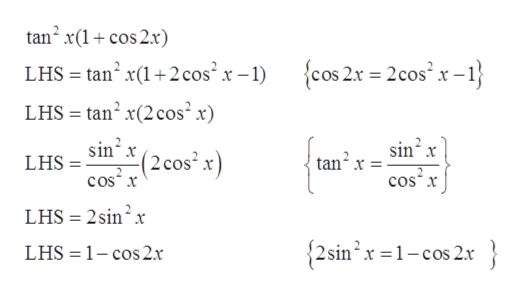



Answered Tan2x 1 Cos2x 1 Cos2x Verify The Bartleby



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com



Sin 2x Cos 2x And Tan 2x




Sin 2 X Cos 2 X 1 Willoughby Len




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com



Pythagorean Identities
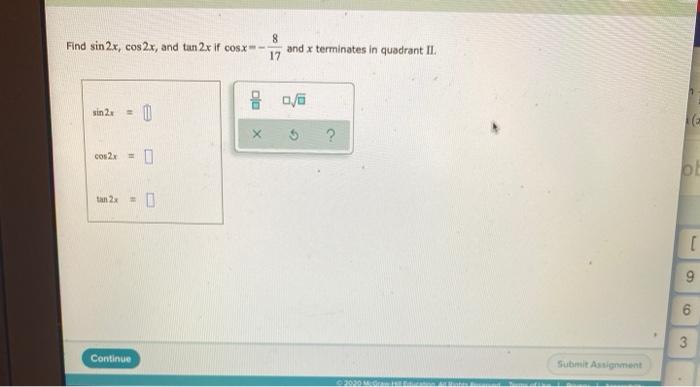



Solved Find Sin 2x Cos2x And Tan 2x If Cosx 8 17 And X Chegg Com
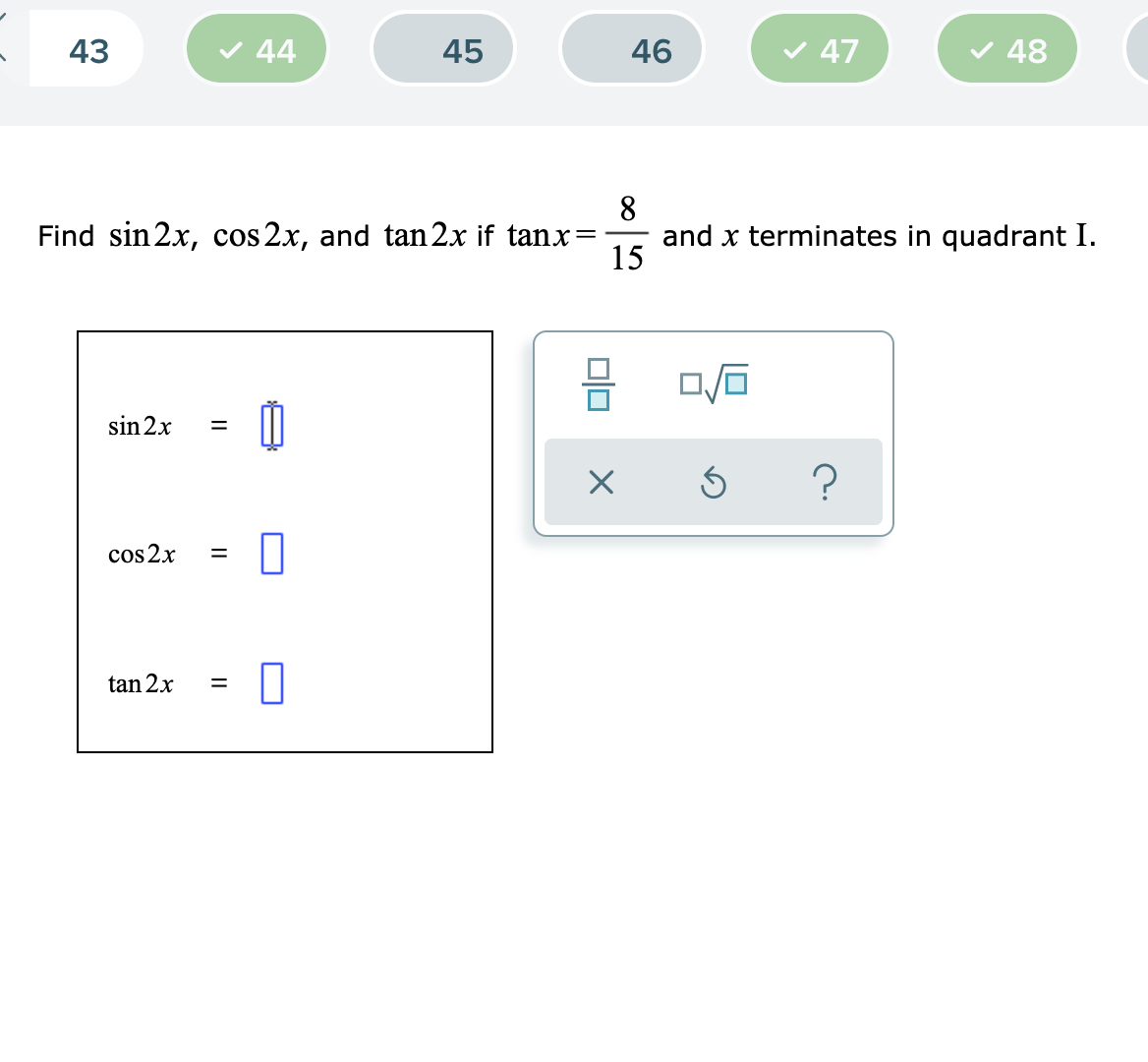



Answered 43 V 44 45 46 V 47 V 48 8 And X Bartleby




Day 3 Hw 1 To 2 Find Sin2x Cos2x And Tan2x Given One Trig Value And The Quadrant Youtube




Analytic Trig Ppt Video Online Download
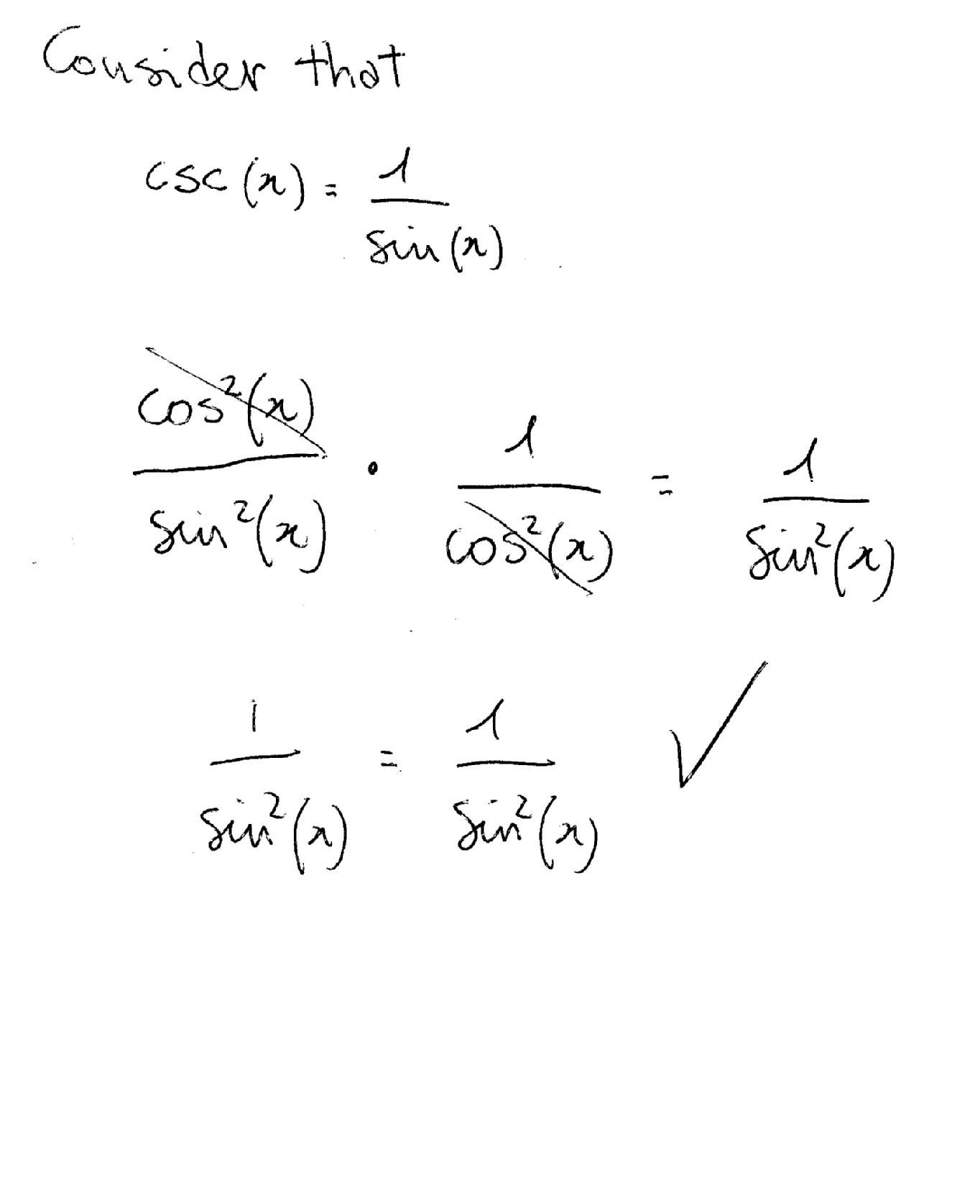



How Do You Verify Cos 2x Sin 2x 1 Cos 2x Csc 2x Socratic



What Is The Formula Of Tan2x Quora



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Trig 2 Caldervale High School



Prove Sin X Sin 3x Cos X Cos 3x Tan 2x Youtube




Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube




Solved Find Sin 2x Cos 2x And Tan 2x If Tanx 5 12 And X Chegg Com



1



Verify Sin 2x 1 Cos 2x Tan X Youtube




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube




Cos2x Sin2x Identity




Sin2x Cos2x 1 Proof




Finding Sin 2x Cos 2x Tan 2x Finding All Solutions Of X Mathematics Stack Exchange




Prove That 1 Sin 2x Cos 2x 1 Sin 2x Cos 2x Tan X Youtube



Tan2x ただの悪魔の画像



Frac Tan 2x1 Tan 2x Cos 2x Sin 2x How To Prove Gauthmath



Tan2x ただの悪魔の画像




Packet 21 Trigonometric Identities Ppt Download




Trigonometric Identity Challenge Sin 2 Cos 2x Tan 2x Youtube



2




Formulas For Sin 2x Cos 2x And Tan 2x And Their Applications Part 7 Youtube




If Tan 2x Cos 2y Sin 2y Prove That Cos 2x Sin 2x Tan 2y Maths Trigonometric Functions Meritnation Com




Solved Try Again Your Answer Is Incorrect Sin 2x Your Chegg Com
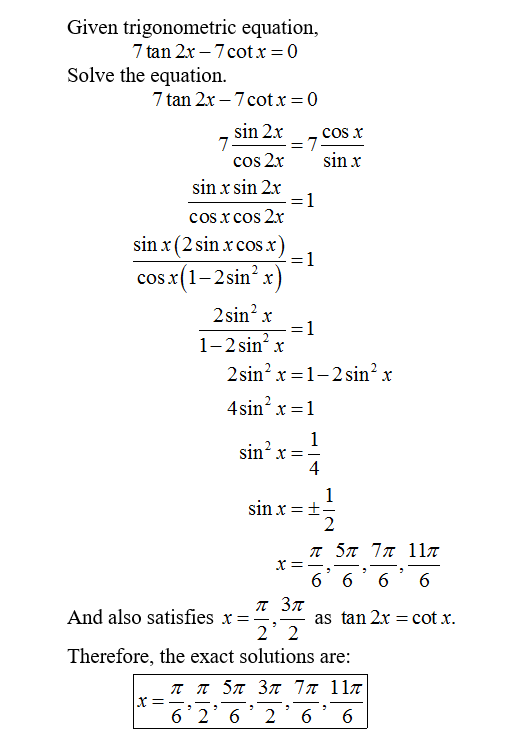



Solved Given Trigonometric Equation 7 Tan 2x 7 Cotx 0 Chegg Com
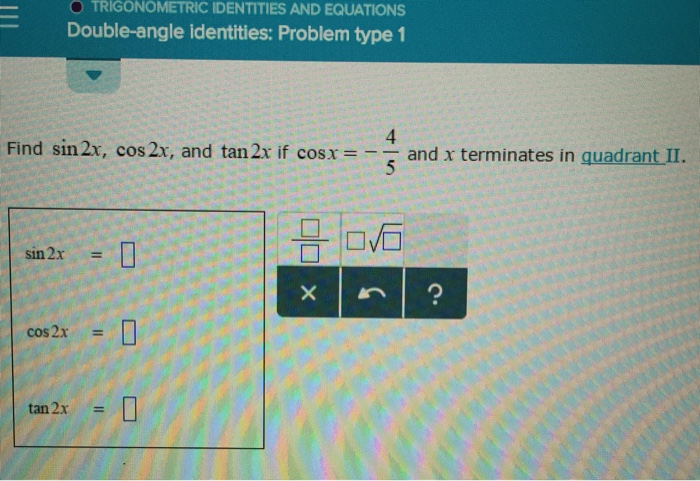



Solved Find Sin2x Cos 2x And Tan 2x If Cos X 4 5 And Chegg Com




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com
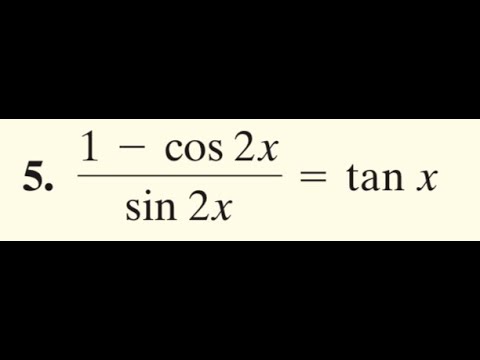



Verify 1 Cos 2x Sin2x Tan X Youtube




Trigonometric Identity 1 Cos2x Sin2x 1 Cos2x Sin2x Tanx Youtube



Sin 2x 1 Cos 2x 2 Csc 2x Tan X



Section 2 Identities Cofunction Double Angle Half Angle Ppt Video Online Download



0 件のコメント:
コメントを投稿